Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Возможна такая механическая аналогия. Малые свободные колебания математического маятника – колебания гармонические. Если приложить к нему вынуждающую силу, меняющуюся со временем, колебания станут вынужденными. Если вынуждающая сила мала, то вдали от резонанса вынужденные колебания будут мало отличаться от свободных. Если же внешнее возмущающее воздействие велико, то закон движения маятника может быть в принципе каким угодно в пределах, которые определяются массой груза, длиной нити и силами трения.

Итак, рост популяции может быть как свободным, так и управляемым. Управляемый рост отличается от свободного наличием управляющей системы , стоящей над популяцией и способной изменять ее свободный рост в тех границах, которые определены биотическим потенциалом популяции и сопротивлением среды.

Например, превратить естественный экспоненциальный рост в рост гиперболический. Поскольку управляемый рост может быть осуществлен только достаточно сложной системой управления, как минимум обладающей памятью, то момент детерминации может быть расположен позднее во времени того момента, когда происходит детерминированное событие.

Понимать это надо так: управляющая система непрерывно контролирует текущую численность популяции и воздействует на внутрипопуляционные связи таким образом, чтобы сделать максимально вероятной последовательность ранжированных событий, каждое из которых заключается в достижении численности популяции в определенный момент времени в будущем некоторого предустановленного значения.

Задача каузального анализа в таком случае заключается в том, чтобы найти целевой, телеологический каузальный закон, управляющий ростом, и механизм его реализации.

Закон степенного роста (убывания) какой-либо величины во времени – это зависимость вида y = C(t – t 0) n, где показатель n не равен нулю или единице и может быть положительным, отрицательным, целым или дробным.

Может ли численность роста какой-либо популяции на каком-то этапе своего роста описываться степенным законом? Это возможно лишь при том условии, что на этом этапе прирост численности за небольшой промежуток времени будет пропорционален некоторой степени численности, причем показатель этой степени не должен быть равен единице.

В таком случае вопрос можно сформулировать так: может ли скорость роста численности популяции выражаться в виде степенного закона (3) рис. 1?

Рис. 1. Степенной и экспоненциальный законы роста численности популяции.

При разных значениях параметра m закон (3) описывает параболический, экспоненциальный и гиперболический рост. Возьмем для определенности значения m = 0, 1, 2, которые соответствует трем наиболее часто встречающимся в природе законам: линейному, экспоненциальному и гиперболическому.

Из них только закон экспоненциального роста имеет встроенный масштаб времени или характерное время удвоения численности популяции, что ясно уже из соображений размерности, т. к. показатель экспоненты представлен в виде произведения константы α, умноженной на время t.

Следовательно, величина обратная α, определяющая этот встроенный масштаб времени, должна иметь размерность времени, поскольку в показателе экспоненты может стоять только безразмерная величина.

Термин «встроенный масштаб времени», возможно, является не совсем удачным, поскольку закон экспоненциального роста не содержит в себе какого-то единственного масштаба, в котором можно измерять время протекания процесса. А содержит постоянную времени через которую этот масштаб: время удвоения численности, какое-то другое характерное время может быть выражен.

Природа экспоненциального роста такова, что если взять произвольную точку на оси времени и откладывать от нее интервалы произвольной, но равной длительности, то численность популяции на последовательности этих интервалов будет расти по закону геометрической прогрессии.

Что в корне отличает его от степенного параболического или гиперболического роста. Для которых не существует встроенного масштаба времени – неизменного времени удвоения численности, т. к. для них это время либо растет, либо убывает.

И которые в силу своих особенностей не могут описывать рост какой-либо популяции, при том условии, конечно, если считать, что они описываются причинными законами, т. е., если полагать, что они порождаются нелинейной положительной обратной связью (НПОС) между численностью и ее естественным приростом. НПОС, причины которой полностью определяются связями (и только связями, а не индивидуальной способностью к размножению) между членами популяции и которая может быть понята́ и описана.

В самой природе степенного роста популяции есть что-то неестественное: трудно себе представить, чтобы прирост численности был пропорционален не самой численности, а какой-то ее степени. При экспоненциальном росте прирост численности популяции пропорционален самой численности. Если удвоить численность, то за этот же промежуток времени удвоится и ее прирост.

Но если прирост зависит от численности по степенному закону – это не так. В таком случае можно попробовать постулировать зависимость коэффициента прироста численности от численности по степенному закону. Открытие закона гиперболического роста населения Земли описывает Л.М. Гиндилис:

«Довольно очевидно, что абсолютный прирост населения должен быть пропорционален численности населения. Если взять какой-то однородный в демографическом отношении регион, то из двух пунктов этого региона, прирост будет выше там, где больше численность населения. Точно так же, чем больше численность населения в момент времени t, тем больше и прирост населения в этот момент. Статистика показывает, что за небольшое время dt, прирост будет равен dN = αNdt…

В 1960 году в журнале «Science» была опубликована статья трех авторов Х. Фостера, П. Мориа и Л. Эмиота, которая называлась «День страшного суда пятница 13 ноября 2026 года». Используя тщательно отобранные статистические данные авторы показали, что относительный прирост населения растет так же быстро, как само население. Чем объясняется такая зависимость, остается пока неясным».

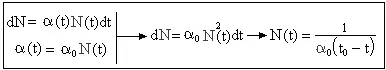
Рис. 2. Пропорциональность коэффициента мирового естественного прироста общей численности народонаселения позволяет объяснить гиперболический рост населения Земли.