Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Если же это условие будет нарушено – экспоненты не получится; например, если для некоторой популяции коэффициент рождаемости – константа и не зависит от численности, а коэффициент смертности пропорционален численности, то рост будет логистическим.

Каким должен быть закон свободного роста изолированной популяции в условиях среды, свойства которой не меняются и при учете взаимодействия ее членов? Будем считать выполненными все возможные идеализации, рассмотренные нами ранее. Для такой популяции прирост за счет рождаемости, так же как и убыль за счет смертности, возрастает при увеличении ее общей численности.

Поэтому в простейшем случае без учета внутривидовых взаимодействий (тех из них, что влияют на прирост численности) скорость роста должна быть пропорционально общей численности. Поскольку даже и при учете взаимодействий, если их влияние устремить к нулю, обобщенный закон роста должен превращаться в уравнение Мальтуса, то дифференциальное уравнение этого закона должно быть уравнением первого порядка.

Процесс роста численности свободной популяции, т. е. популяции, рост которой никем и никак не регулируется, не зависит (при прочих равных условиях) от того на каком участке шкалы физического времени он наблюдается. Поэтому время как независимая переменная не должно явным образом входить в состав его правой части.

Такие уравнения называются автономными. Структура правой части обобщенного закона должна иметь вид (5): линейный член αN плюс нелинейный F(N), описывающий взаимодействие между членами популяции.

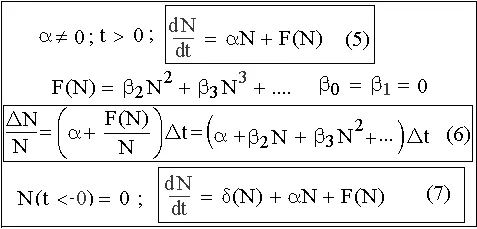
Рис. 1. Обобщенный закон свободного роста изолированной популяции.

Причем значение этой функции при N = 0 должно быть равным нулю: F(0) = 0, т. к. иначе пришлось бы допустить существование составляющей прироста, не зависящей от численности популяции. Так, например, при N = 0, т. е. при полном отсутствии членов популяции, скорость роста была бы не равна нулю. Что противоречит фундаментальному свойству жизни: живое происходит только от живого, и прирост определяется, прежде всего, численностью.

Если все же допустить присутствие аддитивной константы в правой части уравнения (5), то в простейшем случае, если отбросить линейный и нелинейный член и оставить только константу, получим закон линейного роста численности от времени, который не может описывать рост никакой свободно растущей популяции, поскольку прирост здесь является постоянным и никак не зависит от растущей численности. (Это утверждение находится в противоречии с феноменологической теории Капицы, согласно которой скорость роста численности гоминид на первом этапе продолжительностью 2,8 млн лет была постоянной и не зависела от растущей численности.)

Если же оставить линейный член плюс константа от нелинейного – получим простейшее линейное неоднородное дифференциальное уравнение первого порядка с постоянными коэффициентами. В зависимости от знаков С и α имеется четыре варианта роста численности:

Рис. 2. Пример простейших линейных законов, которые не могут описывать свободный рост (убывание) численности популяции.

• Случай С > 0, α > 0 можно интерпретировать как экспоненциальный рост популяции с учетом постоянного дополнительного прироста за счет клонирования. При этом численность популяции неограниченно возрастает.

• Случай С < 0, α > 0 – рост численности популяции рыб в «неограниченном» водоеме с заданной квотой отлова. Численность популяции неограниченно возрастает.

• Для случая С > 0, α < 0 можно предложить такую леденящую душу легенду: вымирающее человечество с отрицательным коэффициентом естественного прироста, постепенно заменяемое киборгами (инопланетянами) с тем же коэффициентом естественного прироста α < 0, что у людей; С – число киборгов, введенных в социум за месяц, αN – число погибших за месяц членов социума (киборгов и людей). При приближении к асимптоте N = -С/α «человеческая составляющая» социума устремляется к нулю.

• Случай С < 0, α < 0 – совсем уже печальный с N = 0 в итоге: планомерное истребление и без того уже вымирающей по естественным причинам популяции.

Все это примеры несвободного, управляемого роста популяции, т. к. в каждом из этих случаев прирост ее численности происходит не только за счет собственной способности популяции к размножению (αNΔt), но и за счет сторонних (управляющих) сил, вносящих постоянный вклад в этот прирост (СΔt). Следовательно, уравнение (4) не может считаться причинным законом, а при α > 0 (т. е. в случае роста популяции) процесс роста, описываемый этим уравнением, не может быть определен как простой автокаталитический, самоускоряющийся процесс.

Итак, уравнение (4) не может служить для описания динамики свободного роста популяции каких-либо организмов из-за присутствия в его правой части аддитивной константы. В дальнейшем будем говорить только о мальтузианской составляющей, определяющей рост популяции, т. е. считаем, что α > 0.

Согласно теореме о разложении функции в степенной ряд, любую «достаточно хорошую» функцию всегда можно в такой ряд разложить. Следовательно, нелинейный член F(N) в правой части уравнения (5) можно разложить в ряд Маклорена; при этом первый и второй член разложения должны быть равны нулю: β o= β 1= 0, т. к. константу отбрасываем, а линейный член равен αN, α > 0.

Полученное уравнение с разделяющимися переменными можно проинтегрировать для каждой конкретной F(N). Отсутствие аддитивной константы в правой части приводит к тому, что она обращается в нуль при N = 0. Т. к. левая часть уравнения – это производная от численности по времени или скорость роста, то для кривой роста имеется горизонтальная асимптота, совпадающая с осью времени, т. е. такая же асимптота, как у экспоненты.

Это хороший показатель, он говорит о том, что рост численности популяции, определяемый обобщенным законом роста в его идеальном описании с непрерывной численностью, не имеет начала. Если бы рост начинался в некоторый фиксированный момент времени, пришлось бы давать какое-то объяснение выделенности этого момента, как, например, при описании степенного параболического роста.

Кроме того, очень важно понимать то, что линейным членом αN в обобщенном уравнении роста (5) пренебречь нельзя в принципе. Перечислим причины, почему это так:

1.Т. к. разложение F(N) начинается с квадратичного члена, то F(N)/αN → 0 при N → 0, откуда следует, что при небольшой численности рост описывается линейным уравнением Мальтуса, является экспоненциальным и не зависит в первом приближении от взаимодействий между членами популяции. Т. е. получается правильная асимптотика.