Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Потом он «округляет» его до трех, хотя средний коэффициент ускорения развития мировых цивилизаций согласно, например, исследованиям академика Ю.В. Яковца равен примерно двум. Свою постоянную времени τ = 42–45 лет С.П. Капица не связывает ни с каким глобальным циклическим историческим процессом, хотя она примерно равна продолжительности, вероятно, самого главного экономического и исторического цикла – Кондратьевского цикла.

Последний цикл его периодизации по длительности также примерно равен τ, а длительность всех остальных выражается целым числом τ. Эту константу он называет временем, «…определяемым внутренней предельной способностью системы человечества и человека к развитию». Что это означает – не понимает никто.

Безразмерную константу K (Kapitsa), которая вводится вместе с τ, он определяет как главное число своей теории и в одних своих работах называет эффективным размером группы людей, а в других – аналогом числа Рейнольдса в гидродинамике. Что означают константы τ и K на самом деле – совершенно непонятно.

В девяностые годы, когда его «феноменология» еще окончательно не закостенела и казалось, что вот-вот, еще чуть-чуть и все станет ясно, он надеялся, что каким-то чудесным образом, возможно, чисто математически: расширением области определения переменных, либо каким-то иным путем эту загадочную цикличность удастся все-таки обосновать:

«Отмеченную цикличность можно связать с тем, что Рв = К 2lnt периодична в комплексной области, или же тем, что мы имеем дело с бифуркациями в более полной системе уравнений, описывающей рост» [1].

Но время шло, а проблема так и оставалась нерешенной. Спустя много лет, все, что может предложить автор «Парадоксов роста» – это лишь поверхностную, механистическую аналогию:

«Хорошо известно, что умело закрученный плоский камень, брошенный под малым углом к поверхности пруда способен многократно отскакивать от воды, совершая прыжки на большое расстояние. В этом явлении мы видим, как быстрое вращение камня стабилизирует его в пространстве, несмотря на удары о поверхность воды. С другой стороны, мы видим, как в этих условиях преобразуется движение камня по инерции и образуется устойчивая периодическая серия укорачивающихся скачков, пока движение не затухнет и камень не утонет.

В этой механической модели можно усмотреть поучительные аналогии с предложенной моделью развития населения Земли, когда внутренние процессы приводят к возникновению периодических циклов, которые определяют развитие и устойчивость этого процесса. Поэтому подобные примеры, взятые из механики, помогают понять развитие такой сложной системы, как человечество, в результате которого население Земли в среднем устойчиво следует по статистически детерминированному пути автомодельного, самоподобного роста, управляемого внутренней динамикой роста, сцепленного с развитием благодаря разуму» [21].

Не находит объяснения эта цикличность и в последней попытке построить модель роста численности населения Земли с учетом пространственного распределения (авторы: В.А. Князева, Е.Н. Белавин, Е.С. Куркина) [119].

Рост численности человечества с учетом пространственного распределения безо всякого обоснования и каких-либо объяснений описывается ими с помощью уравнения диффузии или горения, которое, по их мнению, может описывать и мировой демографический процесс. Путем подгонки по нескольким параметрам они получают необходимое (11) число исторических циклов.

Однако такая прямая подгонка ad hoc не устраивает даже С.П. Капицу, наиболее заинтересованного в данной работе: «Это неубедительно ведь, то, что нужно(выделено мной. – А.М.) просто задается??» Заметим, что Князева, Белавин и Куркина за это свое псевдонаучное «исследование» получили хорошие деньги: на него был выделен грант, вероятно, не без помощи С.П. Капицы.

В последней своей работе «Парадоксы роста…» С.П. Капица «пришел к выводу», что показатель сжатия исторического времени должен быть равен двум (стр. 182). Т. к. за момент начала неолита у него взята дата 9 тыс. лет до н. э., т. е. мало отличается от той, что принята в нашей модели, то не только количество циклов, которых должно быть 15, а не 11, но и разметка исторического времени на эти циклы у него должна быть примерно такой же, как у нас.

На самом деле для коэффициента сжатия исторического времени он получил величину e/(e-1) = 0.583 (1/0.583 = 1.7), которую странным образом округлил до 0.5, что соответствует показателю сжатия, равному двум. При этом автор «Парадоксов роста» не счел нужным упомянуть ни работу Ю.В. Яковца 1997 года, в которой этот показатель равен 1.8, что ближе к двойке, чем у него, ни нашу работу 2006 года, в которой он в точности равен двум. С.П. Капица – и это характерно для его творчества – трудности, которые испытывает его теория, – никак не отмечает, своих ошибок – никогда не признает, на предшественников, как правило, – не ссылается.

Во всех работах С.П. Капицы по теоретической демографии можно найти графики линейного, экспоненциального и гиперболического роста как возможные варианты роста численности человечества:

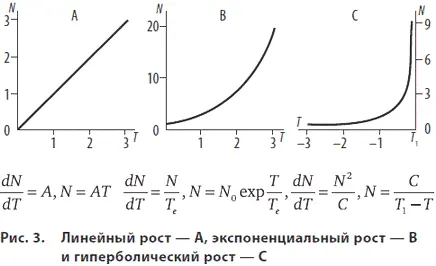
Уравнения роста как причинные законы здесь схожи, но только при гиперболическом росте численность популяции устремляется к бесконечности за конечный промежуток времени, что приводит, по его мнению, к режиму с обострением, выход из которого С.П. Капица, используя терминологию термодинамики, называет фазовым переходом. В этом, считает С.П. Капица, и состоит главный секрет гиперболического роста со всеми необходимыми для его «феноменологии» физикалистскими следствиями.

Представляется совершенно недопустимым ставить в один ряд столь разные для экологии популяций законы роста, один из которых распространен повсеместно, тогда как другие два как причинные законы роста популяций – НИКОГДА не встречаются в природе.

Линейный закон, как мы уже отмечали ранее, дает постоянный, не зависящий от растущей численности прирост, что выглядит как полная несообразность. Гиперболический рост населения Земли, происходящий по причине ПОС второго порядка между численностью и мировым естественным приростом также невозможен, т. к. предполагает для рассредоточенной популяции Homo sapiens системность, которой она никогда не обладала и еще по множеству других причин.

Экология популяций – это не физика, у нее свои законы и главный из них – закон экспоненциального роста, который, по мнению физика (!), лауреата нобелевской премии В.Л. Гинсбурга, является первым и важнейшим законом (или даже принципом) экологии популяций.