Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Рис. 4. Подсчет времени эволюции человека при старте Сети с трех клаттеров.

Это приближенное значение согласуется с данными палеодемографии, согласно которым один миллион лет назад проживало порядка 180 тысяч человек. Модель требует 216 тысяч. Однако этот результат не соответствует периодизации эволюционного процесса согласно прогрессии эволюции, и, кроме того, есть дополнительные соображения, связанные с временем цикла Сети 256, которые не позволяют принять такой сценарий.

Сеть 256 в своей эволюции проходит 173 цикла за время 3,4 млн лет. Постоянная цикла равна примерно 20 тыс. лет, следовательно, где-то за 40 тыс. лет до момента старта Сети человека численность первых представителей рода Homo составляла 65536*1.1 = 72090, что и не соответствует данным палеодемографии. Если же допустить, что рост Сети стартовал с четырех клаттеров, то произошло это событие 0,8 млн лет назад, что не лезет ни в какие ворота. Итак, выбираем первый сценарий и рассмотрим начальные этапы роста Сети.

Определим время эволюции человека как интервал времени, разделяющий момент старта роста Сети человека (с двух клаттеров) и старта Сети вида, следующего за человеком (также с двух клаттеров): T homo= 1,69 млн лет. Здесь же следует отметить, что хотя время репликации и входит в T evol, однако представляется разумным считать, что эволюция любой авангардной системы заканчивается вместе с последним циклом роста ее Сети. (Cм. главу: «Гармонические сети и ноосфера».)

Первый этап роста Сети 65536 от 2-х до 256-ти клаттеров может быть представлен как последовательность звеньев, в момент завершения каждого из которых размер сети увеличивался на единицу. Первая стадия этого процесса при росте Сети от двух до трех клаттеров была самой продолжительной. Она состояла из 65536/4 = 16384 циклов и заняла 16384*39,75 ≈ 650 тысяч лет (копировалось 4 носителя за цикл).

Скорость роста популяции была постоянной и составляла: 4/39,75 ≈ 0,1 человека в год. Постоянство скорости роста связано с первым законом Сети: прирост за цикл, т. е. за 40 лет должен был составлять (по крайней мере в среднем) 4 человека и так на протяжении 16384 циклов. Вторая стадия роста Сети от трех до четырех клаттеров заняла 65536/9 = 7282 цикла и, соответственно, 7282*39,75 ≈ 290 тыс. лет. Средняя скорость роста популяции была равна: 9/39,75 = 0,23 человека в год [12].

Длительность первого исторического периода как времени роста Сети от гармонической с размером 2 до гармонической с размером 4 равно: 650 + 290 = 940 тыс. лет. Точно так же суммируя далее времена роста Сети от гармонического размера до гармонического можно найти все исторические периоды от начала эволюции до второй половины XX века. И если взять отношение длительности каждого предыдущего периода к последующему, то получим следующий числовой ряд:

2.4, 2.2, 2.1, 2.0, 1.9, 1,7, 2.6, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0

Наибольшая степень сжатия периодов гармонического достижения происходит на начальном этапе антропогенеза (2.4) и во время неолита (2.6). Этот числовой ряд и периоды эволюции, с ним связанные, можно разделить на две части:

2.4, 2.2, 2.1, 2.0, 1.9, 1,7, 2.6 – до неолита и неолит.

2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0 – после неолита.

Поскольку после неолита сжатие циклов гармонического достижения происходит в той же пропорции (2 : 1), что и рост размера сети – этот рост идет по простой гиперболе. Чего не скажешь о росте до неолита: здесь коэффициент сжатия не является постоянным, а уменьшается от 2.4 до 1.7 и кривая роста в первой своей части не является гиперболической.

Гиперболой ее можно считать лишь в первом приближении. Но уже и такого представления достаточно, чтобы понять, что единой гиперболы, в соответствии с которой происходил рост населения Земли на всех этапах эволюции и истории – не существует. Разрыв в динамике изменения коэффициента сжатия (1.7 —> 2.6) говорит о том, в эпоху неолита происходит скачок скорости роста и начинается демографический взрыв.

Что касается раннего (нижнего) палеолита, то поскольку никакими более-менее надежными данными по численности наших далеких предков мы не располагаем, то и сравнивать теоретические данные здесь не с чем. Для верхнего палеолита (40—12 тыс. лет назад), когда человек расселился по всей Земле, существуют данные и оценки разной степени надежности, на основе которых Мак-Эведи и Джоунсом [38] была предложена гиперболическая зависимость (4):

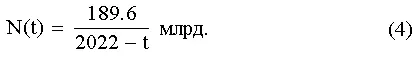
Рис. 1. Гипербола Мак-Эведи и Джоунса.

Сравним теорию с этой гиперболой. Для этого сдвинем начало отсчета времени от начала новой эры к неолиту, а численность будем измерять в клаттерах. За точку отсчета на оси времени возьмем 8154 год до н. э. (255*39,75 = 10136, 10136 – 1982 = 8154, 10136 + 39,75 ≈ 10180).

И для удобства расчетов ищем зависимость от (-t), т. е. отсчитываем время от 8154 года до н. э. в прошлое. Тогда t = 0 – начало неолита, а t = -10180 – точка сингулярности гиперболы демографического роста. С учетом зомби-коэффициента k = 1.1 находим число клаттеров Сети как функцию времени:

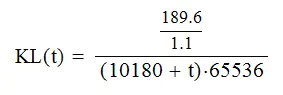
Рис. 2. Зависимость числа клаттеров Сети человека в млрд от (– t) по формуле Мак-Эведи и Джоунса. Время отсчитывается в годах от начала неолита в прошлое.

Алгоритм дает:

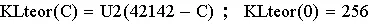
Рис. 3. Зависимость числа клаттеров Сети человека от времени в циклах согласно теории.

Построим в одних координатных осях графики теоретической и эмпирической зависимости числа клаттеров Сети от времени. Время отсчитываем в прошлое в циклах и в логарифмическом масштабе: от 8 тыс. года до н. э. до 1,7 млн лет до н. э. По оси ординат логарифмический масштаб применять не будем для лучшего сравнения.

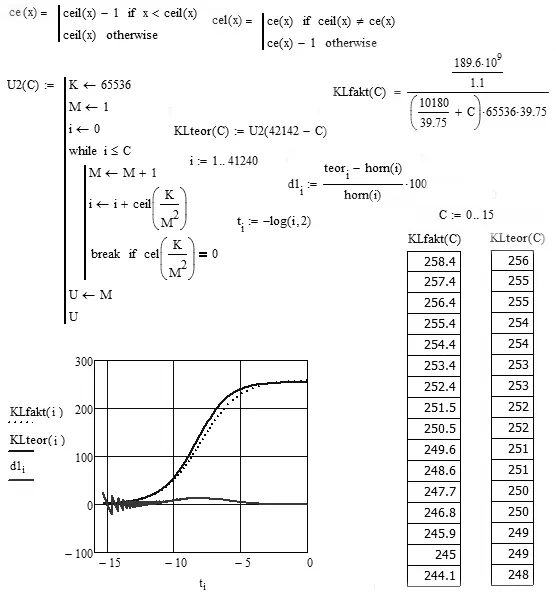
Рис. 4. Сравнение алгоритма теоретической зависимости и гиперболы Мак-Эведи и Джоунса для времен от начала эволюции до неолита.

Алгоритм дает целое число клаттеров, т. е. его погрешность составляет 65536 носителей. Наибольшее отклонение теории от гиперболы (4) равно 11 %. Теоретическая кривая почти не отличается от гиперболы Мак-Эведи и Джоунса, следовательно, теория полностью соответствует имеющимся демографическим данным для времен до 8154 года до н. э. Точность всех дат зависит от точности определения начала перехода: 1982 год (слабо) и от точности, с которой известна постоянная цикла τ = 39.75 лет (сильно).