Александр Волошин - Нейротон. Занимательные истории о нервном импульсе

При этом Гельмгольц допускал, что при движении импульса происходит перемещение каких-то материальных частиц, но ничего более ясного предложить не сумел.

Опытами Гельмгольца наивное представление о нервном волокне как электрическом проводе было опровергнуто. Однако предположить что-то лучшее было не так-то просто. Открытия Гельмгольца поднимали ряд новых вопросов, которые задали работу физиологам на следующие сто лет. На что похожи эти нервные сигналы, впоследствии названные потенциалами действия, и как в них закодирована информация? Как биологические ткани генерируют электрические сигналы? Где идёт электрический ток при этих сигналах?

PS. В современной медицине используется такой метод исследования работы нервной системы – электронейрография – запись электрического сигнала и связанного с ним потенциала действия в момент его распространения вдоль нерва. Применяется для измерения скорости распространения стимула или потенциала действия в нерве. Для проведения электронейрографии периферический нерв стимулируется в одной точке и затем измеряется активность в двух точках на пути её распространения.

В 1879 г. учёный младшего поколения школы Дюбуа-Реймона немецкий физиолог Лудимар Герман ( Ludimar Hermann, 1838 – 1914 ) очень близко подошёл к современным представлениям о математическом описании нервного импульса. Он уподобил его распространение горению бикфордова шнура. Для заданного шнура скорость и форма бегущей по нему уединённой волны горения, очевидно, постоянны (если m – количество пороха, сгорающего в единицу времени, а М – количество пороха в шнуре на единицу его длины, то скорость равна v = m/М; для бикфордова шнура обычно подбирают m и М так, что v = 1 см/с).

Такое сравнение, только на первый взгляд, может показаться наивным и подобным представлениям античных философов. На самом деле, при прохождении импульса, как и при движении пламени, расходуется энергия, которую нужно восполнять, иначе новый импульс не пройдёт. Попробуйте предложить другой пример из физики, в котором бы отправленная в путь волна подпитывалась в процессе своего распространения. Но сравнение это не лишено и недостатков – нервные импульсы при взаимодействии ведут себя иначе, они больше похожи на частицы.

Позднее Герман предложил ещё одну модель, уподобив нерв коаксиальному кабелю 1 1 Электрический кабель с одной центральной жилой. , в котором, однако, волны должны распространяться нелинейно . Решать подобные математические задачи в то время ещё не умели, и даже сам Герман счёл, что математическую теорию нервного импульса разработать невозможно.

К сожалению, он просто не знал об опытах Джона Скотта Рассела ( John Scott Russell, 1808 – 1882 ), который в 1838 году впервые заявил об открытии уединённой (нелинейной) волны которую называют теперь – солитон . Подробное описание этого наблюдения и выполненных им экспериментов было опубликовано в 1844 г. («Доклад о волнах») 2 2 Целенаправленное изучение солитонов началось сравнительно недавно (1960-е гг., работы В. И. Захарова, Л. Д. Фаддеева, Н. Забуски и др.). Тем не менее возможные физические приложения этого феномена уже охватывают многие области современной техники. Наиболее широкое распространение получили оптико-волоконные системы передачи информации. .

Возможно, этот талантливый учёный интуитивно гораздо ближе всех подошёл к открытию реальной природы нервного сигнала, но этого никто не заметил, ни тогда, ни сегодня. А история продолжила развиваться в другом русле на основе выдвинутой им же «теории местных токов» о которой подробно мы поговорим в главе «История мембранной теории».

В 1868 году, Юлиус Бернштейн (Bernstein, 1839—1917), пионер экспериментальной нейрофизиологии, при помощи оригинального устройства, названного реотомом («разрезателем времени»), не только сумел более-менее достоверно измерить скорость распространения нервного импульса, но и экспериментально определил его форму, измерив время нарастания и спада нервного импульса.

А. А. Ухтомский писал, что, идея дифференциального реотома была подсказана Бернштейну Германом Гельмгольцем.

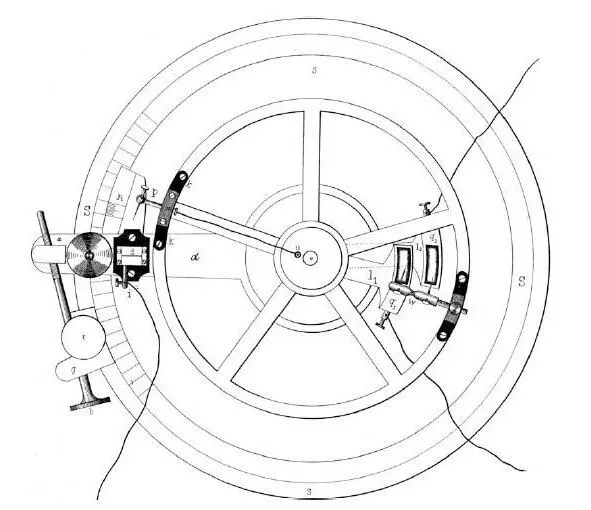
Рисунок 11 Дифференциальный реотом Бернштейна

Прибор представлял собой свободно вращающийся вокруг вертикальной оси диск, снабжённый на периферии двумя штифтами: один – закреплённый неподвижно на диске, путём замыкания и размыкания тока в первичной катушке индукционного аппарата вызывал раздражение объекта, второй – подвижный, для включения тока действия, идущего от объекта в гальванометр.

При вращении диска с известной скоростью препарат раздражается при каждом обороте и на известное время устанавливается сообщение с гальванометром. Если установить контакты таким образом, что замыкание гальванометра происходит в тот же момент, как замыкание и размыкание индукционной катушки, то отклонение гальванометра будет соответствовать начальному фронту тока действия; если же второй штифт, служащий для отведения тока в гальванометр, сдвинуть назад, чтобы при вращении диска он несколько запаздывал от первого, то отведение в гальванометр тока действия произойдёт позднее раздражения объекта.

Путём ряда последовательных сдвигов 2-го штифта можно ответвлять в гальванометр различные фазы возникшего в ткани потенциала и таким образом составить полную картину протекания его в ткани от начала до конца. [10].

Фактические значения скорости распространения возбуждения, найденные с помощью дифференциального реотома, оказались такими же, как и при определении их другими методами. Но значение прибора было не только в этом. Бернштейн, пользуясь этим устройством, определил продолжительность волны возбуждения . На мышце лягушки её продолжительность оказалась примерно 0,05 с, на нерве же около 0,005 с. Для того времени этот результат был довольно точным.

В 1879 году учёный младшего поколения школы Дюбуа-Реймона немецкий физиолог Лудимар Герман ( Ludimar Hermann, 1838 – 1914 ) вплотную подошёл к современному математическому описанию нервного импульса. Он сравнил его распространение с горением бикфордова шнура. Для заданного шнура скорость и форма бегущей по нему уединённой волны горения, очевидно, постоянны (если m – количество пороха, сгорающего в единицу времени, а М – количество пороха в шнуре на единицу его длины, то скорость равна v = m/М; для бикфордова шнура обычно подбирают m и М так, что v = 1 см/с).