Валерий Шевчук - Макроэкономика: конспект лекций

При норме резервных требований, равной 20 %, имея депозиты на сумму 1000 долл., банк должен 200 долл. (1000 долл. ? 0,2 = 200 долл.) хранить в виде обязательных резервов, а остальные 800 долл. (1000-200 = 800) он может выдать в кредит. Однако банк может выдать в кредит только часть этой суммы, например 700 долл. В этом случае 100 долл. (800–700 = 100) составят его избыточные резервы. В результате фактические резервы банка будут равны 300 долл. (200 долл. обязательных резервов + 100 долл. избыточных резервов = 300 долл.).

Если банк хранит избыточные резервы (сверх обязательных), то его норма резервирования будет равна отношению фактических резервов к депозитам ( R факт / D ) и, следовательно, будет представлять собой сумму нормы обязательных резервов и нормы избыточных резервов. В этом случае сумма средств, фактически выданных в кредит ( К факт), будет меньше величины кредитных возможностей банка ( К факт < К ) и может быть подсчитана по формуле

В современных условиях баланс коммерческого банка имеет следующую структуру:

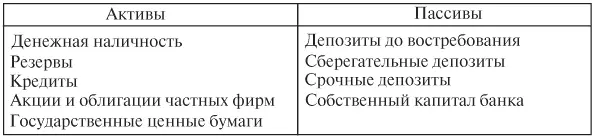
В правой части баланса отражены источники поступления средств (обязательства) и собственный капитал банка, а в левой – направления использования средств вкладчиков. Основным балансовым тождеством коммерческого банка является равенство суммы его обязательств и собственного капитала общей величине активов.

Баланс центрального банка имеет вид:

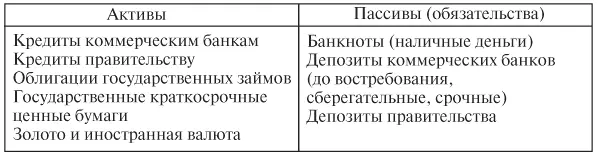
Центральный банк лишь контролирует предложение денег в экономике. Создают же деньги коммерческие банки.

Создание денег коммерческими банками. Банковский мультипликатор.Процесс создания денег коммерческими банками называется кредитным расширением, или кредитной мультипликацией. Он происходит в том случае, если в банковскую сферу попадают деньги и увеличиваются депозиты коммерческого банка, т. е. если наличные деньги превращаются в безналичные. Если величина депозитов уменьшается (клиент снимает деньги со своего счета), происходит противоположный процесс – кредитное сжатие.

При рассмотрении процесса кредитного расширения следует иметь в виду, что:

> во-первых, деньги могут создавать только универсальные коммерческие банки. Ни небанковские кредитные учреждения, ни специализированные банки создавать деньги не могут;

> во-вторых, универсальные коммерческие банки могут создавать деньги только в условиях системы частичного резервирования. Если банк не выдает кредиты, предложение денег не меняется, поскольку количество наличных денег, поступившее на депозит, равно величине резервов, хранимых в сейфе банка. Поэтому происходит лишь перераспределение средств между деньгами, находящимися вне банковской сферы, и деньгами внутри банковской системы в пределах одной и той же величины денежной массы. Благодаря системе частичного резервирования максимальное увеличение предложения денег происходит при условии, что: а) коммерческие банки не хранят избыточные резервы и всю сумму средств сверх обязательных резервов выдают в кредит; это означает, что они используют свои кредитные возможности полностью и норма резервирования равна норме обязательных резервов; б) попав в банковскую сферу, деньги не покидают ее и, будучи выданными в кредит клиенту, не оседают у него в виде наличности, а вновь возвращаются в банковскую систему (зачисляются на банковский счет).

Предположим, что в банк I попадает депозит, равный 1000 долл., а норма обязательных резервов составляет 20 %. В этом случае банк должен отчислить 200 долл. в обязательные резервы ( R обяз = 1000 ? 0,2 = 200) и его кредитные возможности составят 800 долл. ( К = 1000 ? (1–0,2) = 800). Если банк выдаст всю эту сумму в кредит (полностью использует свои кредитные возможности), то его клиент (любой экономический агент, поскольку банк универсальный) получит в кредит 800 долл.

Полученные средства клиент использует на покупку необходимых ему товаров и услуг (фирма – инвестиционных, а домохозяйство – потребительских или на покупку жилья), создав продавцу доход (выручку), который попадет на его (продавца) расчетный счет в другом банке (например, банке II). Банк II, получив депозит, равный 800 долл., отчислит в обязательные резервы 160 долл. (800 ? 0,2 = 160), и его кредитные возможности составят 640 долл. (800 ? (1–0,2) = 640).

Выдав всю эту сумму в кредит, банк даст возможность своему клиенту оплатить сделку (покупку) на эту сумму, т. е. обеспечит выручку продавцу. Сумма в 640 долл. в виде депозита попадет на расчетный счет этого продавца в банке III. Обязательные резервы банка III составят 128 долл. (164 ? 0,2 = 128), а кредитные возможности 512 долл. (640 ? (1–0,2) = 512).

Предоставив кредит на эту сумму, банк III создаст предпосылку для увеличения кредитных возможностей банка IV на сумму в 409,6 долл., банка V – на 327,68 долл. и т. д. Получим своеобразную пирамиду:

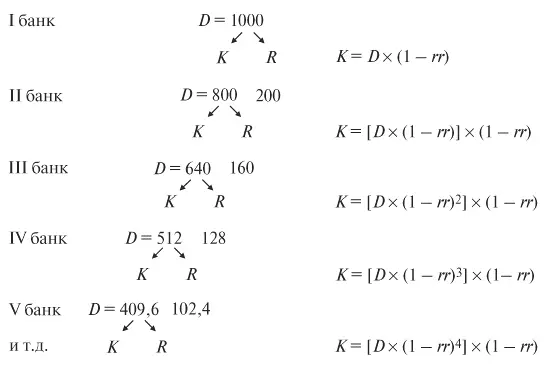
Это и есть процесс депозитного расширения.

Общая сумма денег (общая сумма депозитов банка I, II, III, IV, V и т. д.), созданная коммерческими банками, составит:

Таким образом, мы получили сумму бесконечно убывающей геометрической прогрессии со знаменателем (1 – rr ), т. е. величиной меньше 1. В общем виде эта сумма будет равна:

В нашем случае М = 1000 ? (1 / 0,2) = 1000 ? 5 = 5000. Величина 1 / rr носит название банковского (или кредитного) мультипликатора:

Еще одно его название – мультипликатор депозитного расширения (депозитный мультипликатор). Все эти термины означают одно и то же, а именно: если увеличиваются депозиты коммерческих банков, то денежная масса увеличивается в большей степени, т. е.

Например, в США банковский мультипликатор равен 2,7.