Стюарт Исакофф - Музыкальный строй. Как музыка превратилась в поле битвы величайших умов западной цивилизации

Она называлась “Quid non Ebrietas” и подрывала все устои. Начало было вполне обыкновенным, с интервалами, отталкивающимися от ноты до – именно она казалась здесь опорным тоном, той гаванью, из которой отплывают все мелодические линии. Таким образом, гамма от этого до до следующего служила своего рода музыкальным каркасом произведения. Однако темы в композиции Вилларта не стояли подолгу на одном месте, и вот, спустя мгновение, партия тенора [25] В полифонической музыке Ренессанса тенором назывался голос, ведущий основную тему. в результате неожиданного маневра смещалась к иному тональному центру, с другим набором нот в гамме – а затем и к третьему. Всякий раз, когда музыка, казалось, фиксировалась в некой точке звукоряда, она внезапно сворачивала прочь, бросалась из стороны в сторону, прокладывала новые, неведомые прежде тропинки, затрагивая по пути все двенадцать основных звуков, обрисованных Пифагором в его последовательности чистых квинт. В финале произведения путешествие завершалось скачком на целую октаву.

Эта музыка была полна опасностей – и почти непригодна для исполнения. Даже простую завершающую октаву было непросто спеть. На всем же остальном пути Вилларт коварно расставил непреодолимые препятствия, и главное из них состояло в том, что по мере продвижения от одного тонального центра к другому исполнитель неминуемо натыкался на каждом шагу на музыкальные коммы – те самые неустранимые промежутки, возникающие из-за того, что квинты, октавы и терции рассчитаны по разной пропорциональной мерке. Любой такой промежуток несколько сбивал певца с дороги, и в конечном счете музыка начинала звучать фальшиво, с неприятными на слух интервалами – точно так же, как это произошло бы и на клавиатуре с фиксированными струнами.

Попытка сделать первую и последнюю ноту “Quid non Ebrietas” созвучными друг другу – все равно что попытка наполнить бак объемом в галлон, опорожняя в него то квартовые бочки, то литровые бутылки. Кварта и литр – единицы разных мерных систем, поэтому задача получается невыполнимой: в конечном счете бак либо окажется переполнен, либо, наоборот, наполнен не до конца. Спетая в пифагорейском строе, мелодия Вилларта завершится чудовищно уродливым скачком, на интервал несколько шире чистой октавы; бак будет переполнен. В чистом строе, в связи с присущими ему внутренними несоразмерностями, финальный скачок, напротив, будет меньше чистой октавы – то есть бак останется неполон. Композитор нарочно написал музыку так, что она непригодна для исполнения ни в одной из существующих настроек. Она может быть сыграна и спета лишь в радикальной настройке, которая называется равномерно-темперированным строем.

Всего лишь несколькими десятилетиями ранее мысль о равномерно-темперированным строе показалась бы абсурдной. В этой системе настройки октава делится на двенадцать абсолютно равных частей. Теоретики Средневековья и раннего Возрождения вообще отрицали, что такое возможно. Их кумир и авторитет, Боэций, провозгласил подобную идею заведомо невыполнимой: ведь целый тон – то есть, скажем, расстояние от до до ре – образуется соотношением струн в пропорции 9:8. Его невозможно разделить на две равные части, поскольку такая попытка даст на выходе иррациональное число с бесконечным периодом. Таким образом, нет некоего единого значения, к которому можно было бы привязать до-диез, черную клавишу между до и ре.

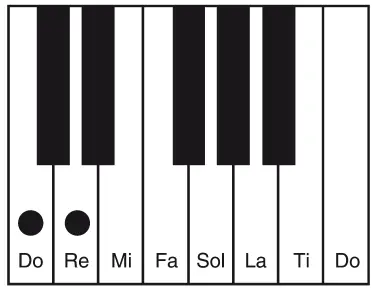
Соответственно, пояснял Боэций, расстояние между до и соседней с ним черной клавишей, до-диез, не может быть таким же, как расстояние между до-диез и ре. Один из этих полутонов (то есть кратчайших расстояний между нотами на клавиатуре) придется образовать соотношением 18:17, а другой – соотношением 17:16. Вместе они действительно произведут верное соотношение целого тона от до до ре – 9:8. Иное решение здесь просто невозможно.

По крайней мере, так казалось до тех пор, пока в 1482 году не вышел перевод “Элементов” Евклида. С Евклидовой помощью удалось найти геометрический выход из сложившегося затруднительного положения – способ решить математическую проблему не через отвлеченные расчеты, а через построение полуокружностей и перпендикуляров. Примененный к монохорду, метод Евклида позволял найти среднее значение между любыми двумя длинами струн: октавами, терциями или даже целыми тонами.

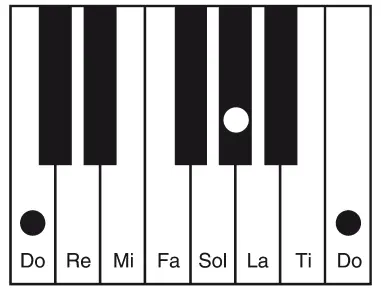
И все же разделение октавы на двенадцать равных частей по-прежнему являлось проблемой: используя Евклидов метод, удавалось разбить любое расстояние на два, четыре, даже на шестнадцать равных интервалов – но не на двенадцать. Этого же можно было добиться, лишь оперируя отдельными частями октавы, но не всей октавой целиком. Например, сработает такой план: восемь равных отрезков малой сексты (от до до ля-бемоль) плюс четыре равных отрезка большой терции (от ля-бемоль до следующего до).

Теоретик музыки Джозеффо Царлино несколько упростил положение в 1558 году, описав мезолябию, изобретение, приписываемое Аристотелю и упоминаемое Витрувием в X веке в его книге об архитектуре. Это механический измерительный прибор с диагональными маркерами, которые движутся по всей длине струн, отмеряя любое желаемое расстояние. Царлино опубликовал инструкции по использованию мезолябии для настройки лютни. Другой похожий метод был разработан Филоном Византийским во и веке до нашей эры; в нем использовались круг и секущая линия. Наконец, еще один похожий способ изобрел уже в XVII веке Марен Мерсенн, задействовав пересекающиеся треугольники. А в крайнем случае можно было всегда использовать методику равномерной темперации, предложенную Джованни Марией Ланфранко в 1533 году: просто уменьшите малые квинты так, “чтобы они звучали не очень приятно для слуха”, советовал он, а большие терции, наоборот, растяните так широко, насколько это возможно. Результат получится более или менее приемлемым!

Так или иначе, доказать возможность равномерно-темперированного строя – еще не значит ввести его в обиход. В самом деле, эта настройка для многих современников Вилларта, надо думать, звучала весьма непривычно. В ней чудесным образом нет “волчьих нот” и других неприятных сюрпризов. Для нашего слуха, привыкшего к современным фортепиано, это идеально подходящий строй. Однако в то время он знаменовал радикальный отход от общепринятых норм. Разделение октавы на двенадцать равных частей изменило пропорции, которые испокон веков использовались для определения различных музыкальных интервалов, – какие-то в большей, какие-то в меньшей степени. Квинты в равномерном строе, к примеру, оказываются ближе к чистым квинтам (3:2), нежели сходные интервалы в среднетоновом строе – зато большие терции “подрихтованы” в семь раз сильнее, а малые терции – в восемь раз. В конечном счете эти изменения вовсе не невыносимы – ни один из получившихся интервалов не звучит некрасиво. Но в сравнении с тем, что было раньше, они могли показаться лишенными изюминки – особенно это касалось больших терций. Яркие и безмятежные в чистом виде, они теперь звучали грубовато и не слишком выразительно.