Иван Рожанский - Античная наука

Помимо чисто математических сочинений, Евклид написал еще ряд сочинений, относящихся, согласно нынешней терминологии, к различным разделам математической физики. До нас дошли: «Явления» («Phaiaonienа»), где излагается элементарная сферическая астрономия; далее, «Оптика» и «Катоптрика», о которых речь пойдет ниже, и «Сечения канона» («Katatome kanonos»), содержавшие десять предложений о музыкальных интервалах. Изложение в этих сочинениях также имело строго дедуктивный характер, причем теоремы в них выводились из точно сформулированных физических гипотез и математических постулатов.

Архимед . Величайший ученый эпохи эллинизма Архимед формально не принадлежал к александрийской научной школе; он родился в 287 до н. э. в Сиракузах и там же прожил почти всю свою жизнь. Считается, однако, несомненным, что он бывал в Александрии, где установил связи с александрийскими учеными; об этом свидетельствует его переписка с Кононом, Досифеем и Эратосфеном.

Будучи сыном сиракузского математика и астронома Фидия, Архимед уже в детстве получил хорошую математическую подготовку. Но собственно математическими проблемами он начал заниматься сравнительно поздно. В какой-то период своей жизни Архимед посетил Александрию, где сблизился с уже упомянутым Кононом (с острова Самос), занимавшим должность астронома при дворе третьего представителя династии Птолемеев — Птолемея III Эвергета (246—211 гг. до н. э.). Конон, в то время находившийся в преклонном возрасте, был, несомненно, высококвалифицированным математиком; предполагается, что именно он побудил Архимеда заняться чисто математическими проблемами. По возвращении в Александрию Архимед регулярно переписывается с Кононом, а после смерти последнего — с его учеником Досифеем. До нас дошли пять писем Архимеда к Досифею; по существу это пять математических трактатов из которых каждый посвящен определенному кругу, проблем в соответствии с их содержанием эти письма-трактаты имеют следующие названия:

1. «Квадратура параболы»,

2 и 3. «О шаре и цилиндре»,

4.«О коноидах и сфероидах»,

5. «О спиралях».

Значение этих писем трудно переоценить: в них Архимед непосредственно подходит к методам высшей математики. Если в первом письме, где решается задача об определении площади параболического сегмента, отсеченного прямой, Архимед еще пользуется методом исчерпывания Евдокса, то в последующих письмах он разрабатывает свой метод, который им применяется к вычислению поверхностей и объемов ряда геометрических тел.

Метод Архимеда представляет собой дальнейшее развитие и усовершенствование метода Евдокса. Как было указано в предыдущей главе, Евдокс получал искомое значение площади (поверхности, объема), безгранично увеличивая число членов ряда величин, сумма которых имела своим пределом именно это значение; Но при этом общая схема метода еще не была сформулирована Евдоксом, и рассуждения должны были повторяться заново для каждого конкретного случая. В отличие от Евдокса Архимед заключал подлежащую определению величину между двумя интегральными суммами, разность которых могла быть сделана меньше любой наперед заданной величины. Искомая величина находится при этом как общий предел обеих сумм при безграничном увеличении числа слагаемых, что эквивалентно задаче о вычислении определенного интеграла. При определении поверхности шара, при нахождении объема сегментов параболоида и гиперболоида, а также эллипсоида вращения Архимед, по существу дела, вычислял интегралы:

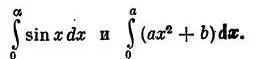
Этим же методом он решал и более трудные задачи — определения длин дуг и площадей ряда кривых поверхностей.

Все эти задачи мы находим в книгах «О шаре и цилиндре», «О коноидах и сфероидах», «О спиралях». Трудно сказать, осознавал ли Архимед, что в каждой из рассмотренных им задач речь шла об одном и том же математическом понятии — понятии определенного интеграла. Во всяком случае, у него еще не было средств, чтобы дать общее определение интеграла. Кроме того, во всех решаемых задачах Архимеда интересовали в первую очередь не методы, а результаты — например, что поверхность шара в четыре раза больше, чем площадь его большого круга, и что объем шара равен 2/3 объема описанного около него цилиндра. Последним результатом Архимед особенно гордился, вследствие чего на его могиле был поставлен надгробный памятник, изображавший шар, вписанный в цилиндр.

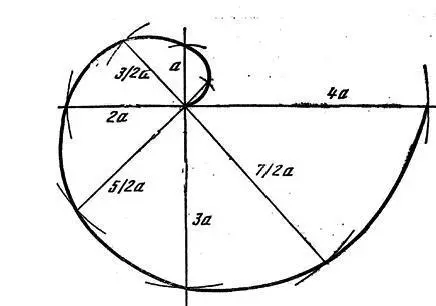
Рис. 7. Архимедова спираль (ρ=αφ)

Наряду с методами вычисления площадей и объемов, Архимед разработал метод определения касательной к кривой, фактически сводящийся к нахождению производной. По каким-то причинам этот метод фигурирует только в письме «О спиралях», где он применяется для определения касательной к спирали ρ=αφ (так называемая «Архимедова спираль», рис. 7), однако рассуждения Архимеда имеют общий характер и применимы к любой дифференцируемой кривой. Тем же методом Архимед пользуется для нахождения экстремальных значений алгебраических выражений, которые могут быть выражены в виде геометрических кривых. В частности, пользуясь современной терминологией, можно сказать, что он провел полное исследование существования положительных корней кубического уравнения определенного вида. Проблема определения экстремальных значений сводится Архимедом к проблеме нахождения касательной к соответствующей кривой.

Помимо пяти писем к Досифею, до нас дошли — полностью или частично — еще некоторые математические работы Архимеда. Так, мы располагаем фрагментом его книги «Измерение круга», в котором доказывается ряд теорем, относящихся к свойствам круга (более полный текст этого сочинения сохранился в арабском переводе). В одной из теорем Архимед пользуется методом исчерпывания, доказывает, что площадь круга равна площади прямоугольного треугольника, один катет которого равен радиусу данного круга, а другой — длине его окружности. При этом в качестве порочного результата Архимед устанавливает приближенное значение отношения длины окружности к диаметру (т. е. числа П). Вычисляя периметры вписанных в круг и описанных вокруг него многоугольников, Архимед устанавливает для этого числа следующие неравенства:

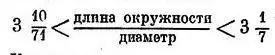
Наряду со строго математическими методами Архимед иногда пользуется остроумными эвристическими приемами для получения тех же результатов. Еще в первом письме к Досифеем («О квадратуре параболы») площадь параболического сегмента определяется не только методом исчерпывания Евдокса, но также «механическим» методом, представлявшим собою изобретение самого Архимеда. Обоснование подобных процедур содержится в рукописи неизвестного ранее сочинения Архимеда, обнаруженной в Константинополе приват-доцентом Петербургского университета Попадопуло Керамевсом и прочтенной в 1906—1908 гг. известным датским филологом И. Л. Хейбергом. В, этом сочинении (так называемый «Эфод»), пользуясь принципом рычага, Архимед приводит доказательства ряда теорем, в других сочинениях доказываемых им с помощью интегрального метода. При этом Архимед пишет: «Кое-что из того, что ранее мною усмотрено при помощи механики, позднее было доказано также и геометрически». Разумеется, такие «механические» методы не могли быть применены ко всем задачам подобного рода, которые, однако, также были решены Архимедом. Механические методы, используемые Архимедом, представляют собой обход интегрирования, когда можно бывает выразить одни интегралы через другие, уже известные. Этому не противоречит то обстоятельство, что механические методы применялись Архимедом задолго до того, как он разработал интегральный метод, представлявший собой развитие метода исчерпывания Евдокса.