Иван Рожанский - Античная наука

Уже в древности большой популярностью пользовалось сочинение Архимеда, дошедшее до нас полностью под названием «Псаммит» (примерный перевод — «Исчисление песчинок») и относящееся к числу поздних работ великого сиракузца, причем, судя по началу, оно было теснейшим образом связано с астрономической проблематикой. Математическое содержание «Псаммита» сводится к разработке системы классификации больших чисел. Эта классификация, кажущаяся теперь неоправданно сложной, заканчивается числом, которое в наших обозначениях может быть записано как 10 8·10^16.

Громадность этого числа должна была поражать воображение древних, не привыкших оперировать с очень большими числами. По сравнению с ним количество песчинок, которые заполнили бы пустую сферу, равновеликую сфере неподвижных звезд, оказалось равным, согласно расчетам Архимеда, неизмеримо меньшему числу — 10 68. Не все математические сочинения Архимеда дошли до нашего времени. Так книги «Леммы», «О семиугольнике», «и касающихся кругах» известны нам лишь в арабском изложении; некоторые геометрические теоремы, доказанные Архимедом, сохранились в математическом трактате знаменитого среднеазиатского ученого Ал-Бируни (973—1048 гг.); от ряда же других книг (в том числе от трактата «О параллельных линиях») до нас дошли лишь их заглавия. Но и того, что нам известно, достаточно, чтобы оценить Архимеда как величайшего математика древности, явившегося предтечей творцов виршей математики Нового времени.

Аполлоний Пергский . Третий великий математик эпохи эллинизма — Аполлоний из Перги (в Памфилии — небольшой области, расположенной на южном побережье Малой Азии) — жил и работал в Александрии, Пергаме и Эфесе в конце III в. до н. э. Наиболее знаменитое сочинение Аполлония — «Конические сечения» («Кonika») - посвящено теории кривых второго порядка эллипса, гиперболы и параболы), получающихся при сечении конуса плоскостью, расположенной под разными углами к оси конуса. До нас сочинение Аполлония дошло не полностью: из составлявших его восьми книг мы располагаемым оригинальным греческим текстом лишь первых четырех и арабским переводом трех последующих; что же касается восьмой книги, то она считается утерянной, хотя о ее содержании мы можем судить по изложению Паппа в его «Математическом сборнике». Долгое время сочинение Аполлония не имело влияния на развитие науки, и лишь в XVII в., в связи с развитием аналитической геометрии, механики и новой теории движения планет, данной Кеплером, наступило возрождение идей Аполлония. Теория конических сечений Аполлония принадлежит к числу таких математических теорий, которые создавались задолго до того, как в них возникала потребность в математическом естествознании.

Из других математических работ Аполлония полностью сохранился (в арабском переводе) лишь один небольшой трактат в двух книгах — «О сечении в данном отношении». В нем рассматривается следующая задача: даны две прямые, лежащие в одной плоскости, и точка на каждой из них; через некоторую третью точку надо провести прямую так, чтобы она отсекала на данных прямых, начиная от данных точек, отрезки, которые находились бы друг к другу в заданном отношении. Первая книга трактата рассматривает случай, когда данные прямые параллельны, вторая — когда они пересекаются (рис. 8). Аполлоний показывает, что эта задача сводится к решению некоторого квадратного уравнения.

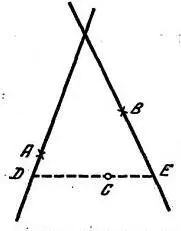
Рис. 8. Теорема Аполлония о сечении в данном отношении.

Аполлоний написал еще два трактата на сходные темы; о них мы знаем по изложению Паппа.

«О сечении с заданной площадью». В этом сочинении рассматривалась задача, аналогичная предыдущей: оба отсекаемых отрезка должны, при умножении их друг на друга, дать прямоугольник заданной площади.

«Об определенном сечении». На прямой даны четыре точки: A, B, С и D. Определить точку Р, лежащую на той же прямой, так, чтобы произведение АР•СР имело заданное отношение к BP•DP.

Несколько трактатов Аполлония известны нам по ссылкам на них Паппа и других позднейших авторов.

«О касаниях». Здесь разбирается знаменитая задача Аполлония: даны три объекта, каждый из которых может быть точкой, прямой или окружностью. Найти окружность, которая проходит через каждую из данных точек и касается заданных прямых или окружностей.

«О плоских геометрических местах». В этом трактате Аполлоний доказывал ряд теорем, в которых рассматривались геометрические места, относящиеся к прямым и окружностям. Некоторые из этих теорем приводятся Паппом. Интересно, что в этом трактате впервые используются инверсия на плоскости и геометрия как преобразования, переводящие «плоские места» (прямые и окружности) в такие же «места».

«О сравнении додекаэдра и икосаэдра». Эта книга упоминается Гипсиклом во введении к так называемой XIV книге «Начал» Евклида. В ней доказывалось, что если додекаэдр и икосаэдр вписаны в один и тот же шар, то их поверхности имеют то же отношение, что и их объемы.

Известны названия еще некоторых сочинений Аполлония, но о их содержании нет определенных сведений. Среди них — работа «О неупорядоченных иррациональностях», в которой, как можно предполагать, классификация иррациональных величин, содержащаяся в «Началах» Евклида, была распространена на более широкие классы иррациональностей. К сожалению, мы не располагаем данными, которые позволили бы судить, насколько далеко Аполлоний продвинулся в этой области.

Но даже из того, что мы знаем о достижениях Аполлония — то ли из его оригинальных текстов, то ли из свидетельств о нем математиков более позднего времени — мы вправе заключить, что в его лице эллинистическая эпоха дала миру первоклассного математического гения. В трудах Аполлония греческая геометрическая алгебра достигла высшего расцвета. После него это направление математической науки начинает постепенно хиреть и иссякать. Для дальнейшего успешного развития античная математика нуждалась в новых импульсах; эти импульсы, однако, нельзя было почерпнуть в тогдашней действительности.

Наряду с гигантскими фигурами Евклида, Архимеда и Аполлония в Александрии и в других культурных центрах III—II вв. до н. э. жили и работали математики меньшего калибра, не давшие новых идей и не разработавшие принципиально новых теорий. И все же некоторые из них заслуживают того, чтобы их имена не были преданы забвению.

О Кононе Самосском, старшем друге Архимеда, мы уже упоминали выше. О его собственных математических достижениях нам ничего не известно; впрочем, он был, по-видимому, скорее астрономом, чем математиком.