Феликс Зигель - Вам, земляне

Точные измерения показали, что ускорение свободного падения на северном полюсе равно 983,234 см/с 2, на экваторе оно примерно на 5,2 единицы меньше. Около 2/3 этой величины обусловлено вращением Земли, а 1/3 — ее сплюснутостью.

Маятниковые часы (или маятник) оказались удивительным прибором, чутко реагирующим на форму Земли и ее вращение. Так практически одновременно с геодезией родилась еще одна отрасль естествознания — гравиметрия — наука о силе тяжести и ее измерении. По гравиметрическим данным, сжатие Земли очень близко к 1: 298,3, что отлично сочетается с данными геодезии.

Но у гравиметрии есть и свои собственные, очень важные в практическом отношении задачи. Представим себе два одинаковых маятника — А и В . Первый из них качается над тем участком земной поверхности, под которым расположены породы повышенной плотности (например, железные руды). Под маятником В внутри земной коры обширная пустота (например, пещера). Какой из маятников колеблется быстрее? Маятник А притягивается Землей (за счет руд) сильнее, чем маятник В. Значит, и колебаться он будет быстрее. Вывод ясен: маятник способен выступать в роли разведчика земных недр. С его помощью можно узнать, где есть ископаемые, каково строение земной коры. Гравиметрия, конечно, решает и другие, практически важные задачи.

При гравиметрических измерениях важно обеспечить постоянство длины маятников, поэтому маятники изготовляют из почти не расширяющегося сплава (инвара), а в последнее время — даже из кварца. Что касается периодов колебаний маятников, то их измеряют высокоточными хронометрами.

Допустим, что один и тот же маятник неизменной длины в двух разных пунктах имеет периоды колебаний Т 1 и Т 2. Тогда соответствующие ускорения силы тяжести g 1 и g 2 связаны формулой g 2=g 1·(Т 2/Т 1).

Эта формула служит основой для относительных измерений силы тяжести, т. е. для сравнения ее значений, полученных в разных точках земной поверхности. Для абсолютных измерений g (в см/с 2) использовали специальные так называемые оборотные маятники, для которых определялись и период, и длина.

Ныне маятниковый метод применяется лишь для решения немногих специальных задач, а абсолютные ускорения свободного падения измеряют методом свободного падения тел в вакууме. При этом ускорение падающего тела измеряют вполне современным способом: расстояния определяют с помощью лазерного интерферометра, а время «засекают» кварцевыми или молекулярными часами. Точность таких измерений очень высокая — средняя квадратическая погрешность не превышает 10 -7м/с 2.

Точно неизвестно, какой была первичная Земля. Однако в любом случае она не была абсолютно твердым телом, а значит, сохраняла способность к деформации, изменению формы под воздействием внутренних и внешних сил. Чтобы лучше представить себе, что тогда происходило, вместо реальной, очень сложной Земли вообразим ее идеализированную модель — исполинскую «каплю» однородной несжимаемой жидкости. Предположим, что внешние силы на эту «каплю» не действуют и ее форма обусловлена только игрой внутренних сил. Если бы «капля» не вращалась, то ее форма определялась бы только взаимным тяготением составляющих частиц, которые стремились бы подойти друг к другу как можно ближе. Это им удалось бы лишь при полной симметрии «капли». Иначе говоря, в этом случае идеализированная модель Земли имела бы форму шара.

В действительности первичная Земля вращалась вокруг своей оси, значит, как показал впервые Ньютон, под действием центробежных сил «капля» сплющилась и приняла форму сфероида. Расчеты Ньютона носили, правда, лишь предварительный, приближенный характер. Гораздо полнее исследования провел его соотечественник Маклорен (XVIII век). Он доказал, что в каждой точке «капли», имеющей форму сфероида, соблюдается равновесие двух противоборствующих сил — взаимного тяготения частиц жидкости и удаляющей их от оси вращения центробежной силы. При этом чем быстрее вращается «капля», тем более сжат сфероид, образуемый ее поверхностью. И шар, и сфероиды Маклорена были названы фигурами равновесия вращающейся однородной несжимаемой жидкости.

Поверхность фигуры равновесия иногда называют поверхностью уровня; она, разумеется, не совпадает с физической поверхностью тела. Для всех этих фигур выполняется одно важное условие: сила тяжести, т. е. равнодействующая силы притяжения и центробежной силы, должна быть во всех точках перпендикулярна к поверхности тела. Только в этом случае любая частица жидкости не будет стремиться двигаться вдоль поверхности тела, а ее давление на лежащие под ней частицы полностью уравновесится силой их противодействия. Именно в этом смысле и надо понимать равновесие сил, определяющих форму жидкой «капли».

В 1834 г. немецкий математик Якоби доказал, что, кроме сфероидов Маклорена, могут быть другие фигуры равновесия жидкой «капли». Оказывается, при достаточно большой угловой скорости вращения сфероиды Маклорена переходят в трехосные эллипсоиды Якоби. Экваториальное сечение эллипсоида (как и его меридиональные сечения) также представляет собой эллипс. Каждый эллипсоид Может быть охарактеризован не двумя (как сфероид), а тремя осями — а, b и с (рис. 5).

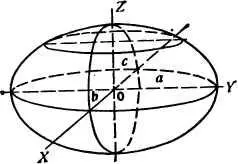
Рис. 5. Трехосный эллипсоид.

Как это ни удивительно, но такая сложная, дынеобразная поверхность, как эллипсоид, может быть устойчивой фигурой равновесия вращающейся однородной несжимаемой жидкости. Более того, как показали исследования Клеро и Стокса, даже для неоднородной жидкости эллипсоиды остаются фигурами равновесия.

Земля, вероятно, никогда не была целиком жидкой и однородной. Но рассмотренная нами идеализированная схема тем не менее к ней применима, так как наша планета никогда не была и абсолютно твердой. Это доказывают результаты геодезических и гравиметрических измерений.

Разные исследователи оценивали сжатие земного сфероида по- разному. И причиной этого были не только погрешности измерений, но и то, что реальная Земля отличная от сфероида и в третьем, более точном приближении к истине, может быть представлена трехосным эллипсоидом.

Разумеется, «дынеобразность» Земли крайне незначительна, и земной экватор мало отличается от окружности. Но все-таки разница есть: наибольший экваториальный диаметр Земли отличается от наименьшего на 140 м. Самый длинный диаметр экватора направлен в точки с долготой 20° к западу и 160° к востоку от начального Гринвичского меридиана, а самый короткий — в точки с долготой 70° к востоку и 110° к западу. Иначе говоря, мореплаватель, находящийся в экваториальных водах Индийского океана, может оказаться на десятки метров ближе к центру Земли, чем его коллега, путешествующий в экваториальной зоне Атлантического океана.