Карл Маркс - Диалектический материализм

Переход к диалектике. Два философских направления: метафизическое с неизменными категориями, диалектическое (Аристотель и в особенности Гегель) — с текучими; доказательства, что эти неизменные противоположности основания и следствия, причины и действия, тожества и различия, бытия и сущности не выдерживают критики, что анализ показывает наличие одного полюса уже in nuce [В зародыше. — Ред .] в другом, что в определенном пункте один полюс переходит в другой и что вся логика развивается лишь из движущихся вперед противоположностей. Это у самого Гегеля мистично, ибо категория является у него чем-то предсуществующим, а диалектика реального мира — ее простым отблеском. В действительности происходит наоборот: диалектика головы — только отражение форм движения реального мира, как природы, так и истории. Естествоиспытатели прошлого столетия, даже до 1830 г., довольно легко обходились еще при помощи старой метафизики, ибо действительная наука не выходила еще из рамок механики, земной и космической. Однако путаницу в умы внесла уже высшая математика, которая рассматривает вечные истины низшей математики как превзойденную точку зрения, утверждает часто вещи, противоположные им, и выставляет теоремы, кажущиеся, с точки зрения низшей математики, простой бессмыслицей. Здесь неизменные категории исчезли, математика вступила на такую почву, где даже столь простые понятия, как «абстрактное количество», «дурная бесконечность», приняли совершенно диалектический вид и заставили математику, против ее воли и без ее ведома, стать диалектической. Нет ничего комичнее, чем жалкие уловки, увертки и фикции, к которым прибегает математика, чтобы разрешить это противоречие, примирить между собою низшую и высшую математику; разъяснить им, что то, что является их бесспорным результатом, не представляет собой чистой бессмыслицы, и чтобы вообще рационально объяснить исходный пункт, метод и конечные результаты математики бесконечного. ( Энгельс, Диалектика природы, стр. 3 — 4, 1932 г. )

Оттого, что нуль есть отрицание всякого определенного количества, он не лишен вовсе содержания. Наоборот, нуль обладает весьма определенным содержанием. Будучи границей между всеми положительными и отрицательными величинами, будучи единственным, действительно нейтральным числом, которое не может быть ни + ни —, он представляет не только очень определенное число, но сам по себе важнее всех других ограничиваемых им чисел. Действительно, нуль богаче содержанием, чем всякое иное число. Прибавленный к любому числу справа, он в нашей системе счисления удесятеряет его. Для этого можно было взять вместо нуля любой другой знак, но лишь при том условии, чтобы этот знак, взятый сам по себе, означал нуль = 0. Таким образом, от природы самого нуля зависит то, что он находит такое приложение и что только он один может найти такое приложение. Нуль уничтожает всякое другое число, на которое его умножают; в качестве делителя какого-нибудь числа он делает его бесконечным, в качестве делимого он делает его бесконечно малым; он — единственное число, находящееся в бесконечном отношении к любому другому числу.0 / 0 может выражать любое число между - 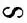и + 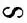и представляет в каждом случае действительную величину. Реальное значение какого-нибудь уравнения обнаруживается лишь тогда, когда все члены его перенесены на одну сторону и уравнение приравнено нулю, как это встречается уже в квадратных уравнениях и употребляется почти всегда в высшей алгебре. Можно какую-нибудь функцию f (x, y) приравнять z и потом дифференцировать этот z , хотя он = 0, как обыкновенную зависимую переменную и получить его частную производную.

Ничто от любого количества само еще количественно не определено, и лишь потому можно оперировать нулем. Те самые математики, которые совершенно спокойно оперируют нулем, как выше указано, т. е. как вполне определенным количественным представлением, и ставят его в количественные отношения к другим количественным представлениям, — поднимают страшный вопль, когда находят у Гегеля такое общее положение: ничто от некоторого нечто есть определенное ничто.

Перейдем теперь к аналитической геометрии. Здесь нуль — определенная точка, начиная от которой одно направление по известной прямой считается положительным, а противоположное — отрицательным. Таким образом, здесь нулевая точка не только так же важна, как любая точка с определенным положительным или отрицательным значением, но и гораздо важнее всех их: это точка, от которой все они зависят, к которой все они относятся, которой они все определяются. Во многих случаях она может браться даже совершенно произвольным образом <���в других случаях, где сама природа данной задачи ставит ограничения, все-таки остается выбор, по крайней мере, между двумя возможностями>. Но раз она взята, она остается средоточием всей операции, часто даже определяет направление линии, на которую наносятся другие точки, конечные точки абсцисс. Если, например, — переходя к уравнению круга, — мы примем любую точку периферии за нулевую точку, то линия абсцисс должна проходить через центр круга. Все это находит приложение также и в механике, где при вычислении движений принятая нулевая точка является опорным пунктом всей операции. <���Произвольно взятая> нулевая точка термометра, — это вполне определенная нижняя граница температурной области, разделяемой на произвольное число градусов и служащей благодаря этому мерой температур как внутри самой себя, так и высших или низших температур. Таким образом, и здесь она является весьма существенной точкой. И даже абсолютный нуль термометра не представляет вовсе чистого абстрактного отрицания, а очень определенное состояние материи, именно границу, у которой исчезает последний след самостоятельного движения молекул и материя действует только в виде массы. Таким образом, где бы мы ни встречались с нулем, он повсюду представляет собой нечто очень определенное, и его практическое применение в геометрии, механике и т. д. показывает, что в качестве границы он важнее, чем все реальные, ограничиваемые им величины. ( Энгельс, Диалектика природы, стр. 115 — 117, 1932 г. )

Асимптоты . Геометрия начинает с открытия, что прямое и кривое представляют абсолютные противоположности, что прямого нельзя совершенно выразить в кривом, кривого в прямом, что они несоизмеримы между собой. И однако уже круг можно вычислить лишь в том случае, если выразить его периферию в виде прямых линий. В случае же кривых с асимптотами прямое совершенно растворяется в кривом и кривое в прямом; точно так же исчезает и представление о параллелизме: линии не параллельны, непрерывно приближаются друг к другу и все-таки никогда не пересекаются. Ветвь кривой становится все прямее, не делаясь никогда окончательно прямой. Точно так же в аналитической геометрии прямая линия рассматривается как кривая первого порядка с бесконечно малой кривизной. Сколь бы большим ни сделалось -x логарифмической кривой, y никогда не станет = 0 . ( Энгельс, Диалектика природы, стр. 31, 1932 г. )