Карл Маркс - Диалектический материализм

Ньютонов параллелограмм сил в солнечной системе истинен, несомненно, для того момента, когда кольца отделяются , потому что вращательное движение приходит здесь в противоречие с самим собой, являясь, с одной стороны, в виде притяжения, а с другой — в виде тангенциальной силы. Но лишь только произошло это отделение, движение опять является доказательством диалектического процесса, — доказательством того, что это обособление должно произойти . ( Энгельс, Диалектика природы, стр. 33, 1932 г. )

Нулевые степени . Их значение в логарифмическом ряду: .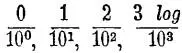

Все переменные переходят где-нибудь через значение единицы, поэтому также и константа какой-нибудь переменной степени, a x= 1 , когда x = 0. a 0= 1 означает попросту, что единицу надо взять в связи с другими членами ряда степеней a . Только в этом случае это имеет смысл и может дать полезные результаты 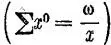, в противном случае — нет. Отсюда следует, что и единица, как бы она ни казалась тожественной самой себе, заключает в себе бесконечное многообразие, ибо она может быть нулевой степенью любого другого числа; а что это многообразие отнюдь не мнимое, обнаруживается во всех случаях, когда единица рассматривается как определенная единица, как один из переменных результатов какого-нибудь процесса (как моментальная величина или форма некоторой переменной) в связи с этим процессом. ( Энгельс, Диалектика природы, стр. 31, 1932 г. )

Прямое и кривое . В дифференциальном исчислении они в конечном счете приравниваются друг к другу. В дифференциальном треугольнике, гипотенузой которого является дифференциал дуги (в методе касательных), эту гипотенузу можно рассматривать «как маленькую прямую линию, являющуюся одновременно элементом дуги и элементом касательной», независимо от того, рассматривают ли кривую как состоящую из бесконечно многих прямых линий или также [Цитата приводится по-французски.] «как строгую кривую, ибо так как искривление в каждой точке М бесконечно мало, то последнее отношение элемента кривой к элементу касательной есть, очевидно, отношение равенства ». Итак, хотя здесь отношение непрерывно приближается к отношению равенства, но приближается по природе кривой асимптотическим образом , так как соприкасание ограничивается не имеющей длины точкой , однако в конце концов принимается, что достигнуто равенство кривой и прямой. Bossut, Calcul diff. et. int. Paris, An VI, I, стр. 149. В случае полярных кривых дифференциально мнимая абсцисса рассматривается даже как параллельная реальной абсциссе, и на этой основе производят действие, хотя обе пересекаются в полюсе; отсюда даже умозаключают о подобии двух треугольников, из которых один имеет угол как раз в точке пересечения обеих линий, на параллелизме которых основывается все подобие!..

Когда таким образом исчерпывается математика прямого и кривого, то открывается новое, почти безграничное поприще, т. е. математика, которая рассматривает кривое как прямое (дифференциальный треугольник), и математика, которая рассматривает прямое как кривое (кривая первого порядка с бесконечно малой кривизной). О, метафизика! [Этот абзац написан позже на полях.] ( Энгельс, Диалектика природы, стр. 31 — 32, 1932 г. )

Из области математики . Ничто, кажется, не покоится на такой непоколебимой основе, как различие между четырьмя арифметическими действиями, являющимися элементами всей математики. И, однако, умножение является сокращенным сложением, деление — сокращенным вычитанием определенного количества одинаковых чисел, а в известном случае — если делитель есть дробь — деление заменяется умножением на обратную дробь. В алгебре идут еще дальше этого. Каждое вычитание (a-b) можно рассматривать как сложение (-b+a), каждое деление a / b как умножение a × 1 / b . При действиях со степенями идут еще дальше. Все неизменные различия способов вычисления исчезают, все можно изобразить в противоположном виде. Степень — в виде корня 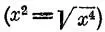, корень — в виде степени 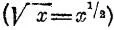. Единицу, деленную на степень или на корень, — в виде степени знаменателя .

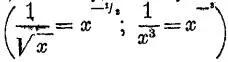Умножение или деление степеней какой-нибудь величины превращается в сложение или вычитание их показателей. Каждое число можно рассматривать и представить в виде степени всякого другого числа (логарифмы, ). И это превращение из одной формы в другую, противоположную, вовсе не праздная игра, — это один из самых могучих рычагов математического знания, без которого в настоящее время нельзя произвести ни одного сколько-нибудь сложного вычисления. Достаточно только вычеркнуть из математики отрицательные и дробные степени, чтобы убедиться, что без них далеко не уйдешь.

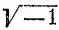(- × - = +, - / - = +, и т. д. раньше развить).

Поворотным пунктом в математике была декартова переменная величина . Благодаря этому в математику вошли движение и диалектика и благодаря этому же стало немедленно необходимым дифференциальное и интегральное исчисление , зачатки которого вскоре были заложены и которое было в целом завершено, а не открыто, Ньютоном и Лейбницем [Этот абзац написан позже на полях.]. ( Энгельс, Диалектика природы, стр. 30 — 31, 1932 г. )

Тожество и различие . Диалектическое отношение их имеется уже в дифференциальном исчислении, где бесконечно мало, но в то же время действенно и производит все. ( Энгельс, Диалектика природы, стр. 30, 1932 г. )

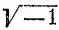. Отрицательные величины алгебры реальны лишь постольку, поскольку они относятся к положительным величинам, реальны лишь в своих отношениях к последним; взятые вне этого отношения, сами по себе, они мнимы. В тригонометрии и аналитической геометрии, вместе с построенными на них отраслями высшей математики, они выражают определенное направление движения, противоположное положительному направлению. Но можно с одинаковым успехом отсчитывать синусы и тангенсы как в первом, так и в четвертом квадратах и значит можно обратить плюс в минус. Точно так же в аналитической геометрии можно отсчитывать абсциссы в круге, либо начиная с периферии, либо начиная с центра и вообще у всех кривых в направлении, обозначаемом обыкновенно минусом, и при этом мы получаем правильное рациональное уравнение кривой. Здесь + существует только как дополнение - , и обратно. Но алгебра в своих абстракциях рассматривает их как действительные, самостоятельные величины, без отношения к какой-нибудь большей , положительной величине. ( Энгельс, Диалектика природы, стр. 111, 1932 г. )