Анатолий Фоменко - Числа против лжи.

Сегодня датировка «древних» затмений используется в некоторых астрономических исследованиях. Например, в теории движения Луны известен параметр D″ — так называемая вторая производная лунной элонгации, характеризующая ускорение. Напомним, что такое элонгация. На рис. 2.1 показана орбита Земли вокруг Солнца и орбита Луны вокруг Земли. Угол между векторами ЗС и ЗЛ называется лунной элонгацией D. То есть, угол между лучами зрения с Земли на Солнце и на Луну. Он, очевидно, зависит от времени. Справа на рисунке показана элонгация, например, Венеры. Максимальной элонгацией называется такой угол, когда луч зрения З'В' с Земли на Венеру касается орбиты Венеры. Надо отметить, что хотя орбиты на рис. 2.1 показаны окружностями, на самом деле они эллиптические. Но поскольку эксцентриситет невелик, то эллипсы условно изображены здесь окружностями.

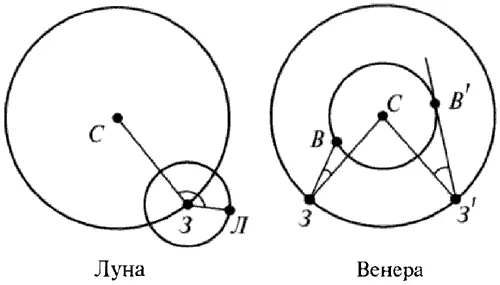
Рис. 2.1. Элонгация Луны — это угол между векторами ЗС и 3Л. Элонгация Венеры — это угол между векторами ЗС и ЗВ. Максимальная элонгация Венеры — угол между З'С и З'В'.

Для некоторых вычислительных астрономических задач полезно знать поведение ускорения Луны в прошлом. Проблема вычисления D″ на большом временном интервале, как функции времени, обсуждалась в дискуссии, организованной в 1972 году Лондонским Королевским Обществом и Британской Академией Наук [1453]. В основу вычисления параметра D″ была положена следующая схема. Для подсчета параметров уравнения движения Луны, в частности D″, берутся их современные значения и варьируются так, чтобы теоретически вычисленные характеристики древних затмений более точно совпали с характеристиками, приводимыми в древних документах для датированных затмений. Для расчета самих дат затмений параметр D″ игнорируется. Это объясняется тем, что дата затмения является более грубым параметром, для вычисления которого точное значение ускорения Луны знать не обязательно. Изменение ускорения Луны влияет на более тонкие характеристики затмения, например, может немного сместить в ту или иную сторону полосу затмения, то есть ту линию, которую прочерчивает на земной поверхности тень Луны во время затмения.

Зависимость D″ от времени была вычислена известным американским астрономом Робертом Ньютоном [1303]. По его мнению, параметр D″ хорошо «определяется большим количеством данных, даты которых пробегают интервал от (— 700) г. до настоящего времени» [1304], с. 113. Роберт Ньютон вычислил 12 значений параметра D″, основываясь на 370 наблюдениях «древних» затмений. Поскольку Р. Ньютон полностью доверял скалигеровской хронологии, то естественно, что он взял даты затмений из скалигеровских хронологических таблиц. Результаты Р. Ньютона, скомбинированные с результатами Мартина, обработавшего около 2000 телескопических наблюдений Луны за период 1627–1860 годы (всего 26 значений), позволили построить экспериментальную кривую зависимости D″ от времени. Эта кривая показана на рис. 2.2.

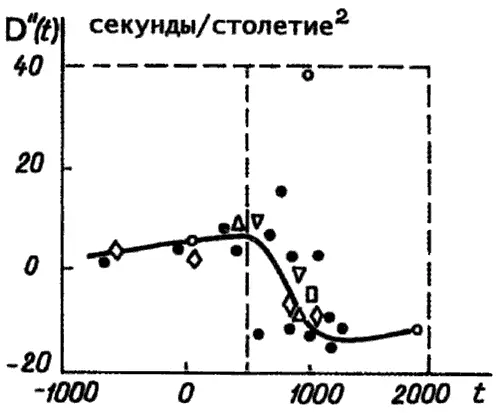
Рис. 2.2. График, D″, вычисленный Робертом Ньютоном. Параметр D″ делает неожиданный скачок на интервале якобы VI–XI веков н. э. Взято из [1303], [1304]. Параметр D″ измеряется здесь в секундах/столетие 2.

Р. Ньютон писал: «Наиболее ПОРАЗИТЕЛЬНЫМ событием… является стремительное падение D″ от 700 года (н. э. — А.Ф. ) до приблизительно 1300 года… Это падение означает, что существует „квадратичная волна“ в оскулирующем значении D″… Такие изменения в поведении D″, и на такие величины, НЕВОЗМОЖНО ОБЪЯСНИТЬ на основании современных геофизических теорий» [1304], с. 114; [1453]. Специальная работа Роберта Ньютона «Астрономические доказательства, касающиеся негравитационных сил в системе Земля-Луна» [1303] также посвящена попыткам объяснения этого загадочного разрыва, скачка на порядок в поведении D″. Надо отметить, что эти таинственные «негравитационные силы», существование которых был вынужден предположить Роберт Ньютон, НИКАКИМ ДРУГИМ ОБРАЗОМ СЕБЯ НИГДЕ БОЛЬШЕ НЕ ПРОЯВИЛИ.

Изучая получившийся график, Р. Ньютон был вынужден отметить, что «от (— 700) г. до (+ 500) г. величина D″ была, возможно, наименьшей по сравнению с теми значениями D″, которые имели место в любой момент на протяжении последних 1000 лет» [1304], с. 114.

И далее, Р. Ньютон писал: «Эти оценки, скомбинированные с современными данными, показывают, что D″ может иметь удивительно большие значения и, кроме того, он подвергался БОЛЬШИМ И ВНЕЗАПНЫМ ИЗМЕНЕНИЯМ на протяжении последних 2000 лет. Он даже изменил знак около 800 года» [1453], с. 115.

Вывод. 1) В якобы V веке н. э. якобы начинается резкое падение, скачок, причем на порядок, величины D″. 2) Начиная с XI века и далее, значения параметра D″ становятся более или менее постоянными и близкими к его современному значению. 3) На интервале якобы V–XI века наблюдается значительный разброс значений D″.

Этот странный факт, оказывается, получает естественное объяснение в новой хронологии.

Дадим краткую сводку сведений, полезных для лучшего пони мания настоящей главы. Более подробную информацию можно извлечь, например, из [534].

Когда Луна при движении вокруг Земли попадает в конус земной тени, на Земле, — а точнее, на ее ночном, обращенном к Луне полушарии, — наступает лунное затмение. Оно наблюдается из любой точки ночного полушария Земли. Затмение длится не более трех часов и возможно только в полнолуние, однако из-за неправильностей движения Луны происходит не каждое полнолуние. В повторяемости лунных затмений имеется грубая, приблизительная периодичность, называемая саросом. Период сароса равен приблизительно 18 годам. В течение этого срока бывает около 28 затмений Луны, так что практически вблизи любого заданного года можно найти хотя бы одно лунное затмение. Сарос довольно легко обнаруживается за 50–60 лет систематических наблюдений, поэтому он мог быть известен уже на заре развития астрономии. Предсказание лунных затмений по саросу все же не очень надежно, и не только из-за неточности сароса, но и потому, что затмение может произойти в тот момент, когда в данной точке земной поверхности стоит день и Луна не видна.

Солнечное затмение наступает, когда наблюдатель оказывается в конусе тени Луны. Если Луна полностью закрывает солнечный диск, то в месте наблюдения наступает темнота и становятся видными звезды. Это — полное затмение. Продолжительность полного солнечного затмения в точке наблюдения не более 8 минут в экваториальной зоне и не более 6 минут в средней зоне. Тень Луны движется по поверхности Земли со скоростью около 110 м/сек, прочерчивая узкую полосу. Ширина этой полосы не превышает 4 градусов. Полоса полной тени окаймлена полосой полутени, ширина которой в одну сторону от середины полосы полной тени-оси затмения — составляет около 30 градусов в средней зоне и около 15 градусов в экваториальной зоне. Наблюдатель в полосе полутени видит солнечный диск, лишь частично закрытый Луной. Это — частное затмение. Максимальная степень покрытия диска Солнца Луной называется глубиной затмения, или фазой. Фаза оценивается обычно в баллах b, который вычисляются по формуле b = 12h, где h — отношение части диаметра Солнца, покрытого тенью, ко всему диаметру. Полное солнечное затмение имеет, следовательно, фазу в 12 баллов. Солнечное затмение фиксируется глазом как потемнение диска, начиная с фазы 3″-4″ балла.