Анатолий Фоменко - Числа против лжи.

Итак, сравнивая летописи X и Y, можно считать, что оба вектора a(X) = (x 1,…, x n) и a(Y) = (y 1,…, y n) имеют одно и то же число координат и поэтому лежат в одном и том же евклидовом пространстве R n. Отметим, что у каждого из этих векторов сумма его координат — одна и та же и равна B-А = D-С, то есть длине интервала времени (А, В). Итак:

X 1+ … + x n= y 1+ … y n= В - А.

Рассмотрим теперь множество всех целочисленных векторов с = (c 1,…, c n), у которых все координаты неотрицательны и их сумма c 1+ … + c nравна одному и тому же числу, а именно B-А, то есть длине временного интервала (А, В). Обозначим множество всех таких векторов через S. Геометрически эти векторы можно изобразить так. Будем считать, что все они выходят из начала координат, то есть из точки O в R n. Рассмотрим концы всех таких векторов с = (c 1,…, c n). Все они лежат на «многомерном симплексе» L, определяемом в пространстве R nодним уравнением c 1+ … + c n= B - А, где все координаты c 1,…, c nявляются вещественными неотрицательными числами. Множество S геометрически изображается как множество «целых точек» на симплексе L, то есть множество всех точек из L, имеющих целочисленные координаты.

Ясно, что концы векторов локальных максимумов a(X) и a(Y) для летописей X и Y принадлежат множеству S, рис. 5.7.

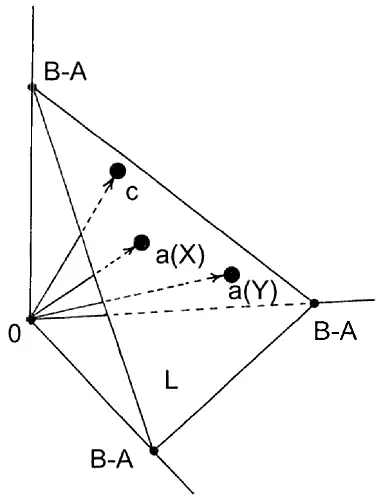
Рис. 5.7. Векторы локальных максимумов а(X) и a(Y) двух сравниваемых летописей X и Y можно условно изобразить двумя векторами в евклидовом пространстве.

Фиксируем теперь вектор a(X) = (x 1,…, x n) и рассмотрим все векторы с = (c 1,…, c n) с вещественными координатами, принадлежащие симплексу L и такие, что они удовлетворяют еще одному дополнительному соотношению:

(c 1 - x 1) 2+ … + (c n - x n) 2≤ (y 1 - x 1) 2+ … + (y n - x n) 2

Множество всех таких векторов с = (c 1,…, c n) обозначим через К. Математически эти векторы описываются как удаленные от фиксированного вектора а(X) на расстояние, не превышающее расстояния r(X, Y) от вектора а(X) до вектора a(Y). Говоря здесь о расстоянии между векторами, мы имеем в виду расстояние между их концами. Напомним, что величина

(y 1 - x 1) 2+ … + (y n - x n) 2

равна квадрату расстояния r(X, Y) между векторами а(X) и a(Y).

Поэтому множество K — это часть симплекса L, попавшая в «n-мерный» шар радиуса r(X, Y) с центром в точке a(X).

Подсчитаем теперь, сколько «целочисленных векторов» содержится в множестве K и сколько — в множестве L. Полученные числа обозначим через m(К) и m(L) соответственно. В качестве «предварительного коэффициента» p'(X, Y) мы возьмем отношение этих двух чисел, то есть

p'(X, Y) = m(K)/m(L),

то есть

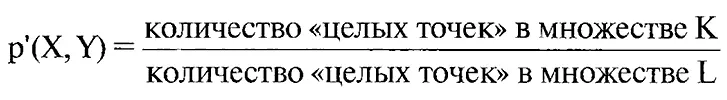
Так как множество К составляет лишь часть множества L, то число р'(X, Y) заключено на отрезке [0,1].

Если векторы a(X) и a(Y) совпадают, то р'(X, Y) = 0. Если векторы, напротив, далеки друг от друга, то число р'(X, Y) близко к единице и даже может оказаться равным единице.

Отметим здесь полезную, хотя и необязательную для дальнейшего, интерпретацию числа р'(X, Y). Предположим, что вектор с = (c 1,…, c n) случайным образом пробегает все векторы из множества S, причем он с одинаковой вероятностью может оказаться в любой точке этого множества. В таком случае говорят, что случайный век тор с = (c 1,…, c n) распределен РАВНОМЕРНО на множестве S, то есть на множестве «целых точек» (n-1) — мерного симплекса L. Тогда определенное нами число р'(X, Y) допускает вероятностную интерпретацию. Оно просто равно вероятности случайного события, заключающегося в том, что случайный вектор с = (c 1,…, c n) оказался на расстоянии от фиксированного вектора а(X), не превышающем расстояния между векторами а(X) и a(Y). Чем меньше эта вероятность, тем менее случайна наблюдаемая нами близость векторов a(X) и a(Y). Другими словами, в этом случае их близость указывает на наличие какой-то зависимости между ними. И зависимость тем больше, чем меньше число р'(X, Y).

Равномерность распределения случайного вектора с = (c 1,…, c n) на симплексе L, — точнее, на множестве S его «целых точек», — может быть обоснована тем, что этот вектор изображает расстояния между соседними локальными максимумами функции объема «глав» исторических летописей или каких-то аналогичных текстов, описывающих заданный период времени (А, В). При рассмотрении всевозможных летописей, говорящих об истории всевозможных государств во всевозможные исторические эпохи, естественно предполагать, что локальный максимум может «с равной вероятностью» появиться в произвольной точке временного интервала (А, В).

Описанное построение выполнено в предположении, что мы фиксировали некоторый вариант введения кратных максимумов у графиков объема летописей. Таких вариантов, конечно, много. Рассмотрим все такие варианты и для каждого из них подсчитаем свое число р'(X, Y), после чего возьмем наименьшее из всех получившихся чисел. Обозначим его через р''(X, Y). То есть, мы минимизируем коэффициент р'(X, Y) по всем возможным способам введения локальных максимумов у графиков vol X(t) и vol Y(t).

Наконец, вспомним, что при подсчете коэффициента р''(X, Y) летописи X и Y оказались в неравноправном положении. Дело в том, что выше мы рассматривали «n-мерный шар» радиуса r(X, Y) с центром в точке а(X). Чтобы устранить возникшее неравноправие между летописями X и Y, просто поменяем их местами и повторим описанную конструкцию, взяв теперь за центр «n-мерного шара» точку a(Y). В результате получится некоторое число, которое мы обозначим через p''(Y, X). В качестве окончательного «симметричного коэффициента» р(Х, Y) возьмем среднее арифметическое чисел p''(X, Y) и p''(Y, X), то есть

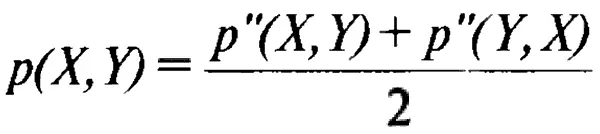
Для наглядности поясним смысл предварительного коэффициента р'(Х, Y) на примере графиков объема с всего лишь двумя локальными максимумами. В этом случае оба вектора

a(X) = (х 1, х 2, х 3) и a(Y) = (у 1, у 2, у 3)

являются векторами в трехмерном евклидовом пространстве.

Их концы лежат на двумерном равностороннем треугольнике L, отсекающем от координатных осей в пространстве R 3одно и то же число B-А. См. рис. 5.8. Если расстояние от точки а(X) до точки a(Y) обозначить через |а(X)-a(Y)|, то множество К — это пересечение треугольника L с трехмерным шаром, центр которого находится в точке а(X), а радиус равен |а(X)-a(Y)|. После этого нужно подсчитать количество «целых точек», то есть точек с целочисленными координатами, в множестве К и в треугольнике L. Взяв отношение получившихся чисел, мы и получим коэффициент p'(X, Y).

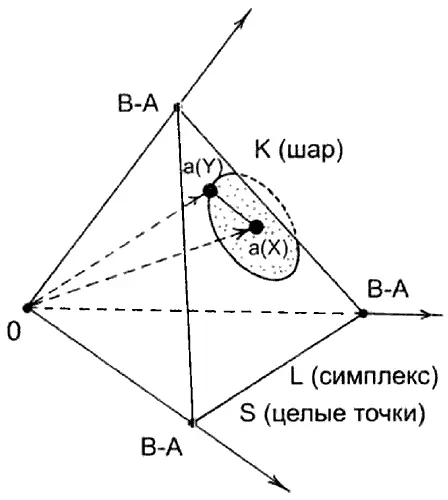
Рис. 5.8. Векторы а(X) и a(Y) определяют «шар», часть которого попадает в симплекс L.