Антон Платов - Мегалиты Русской равнины

Вернемся к каменным кругам. Достаточно легко представить, как создавались каменные круги, имеющие форму правильной окружности. Для этого нужно вбить в центре будущего круга деревянный кол; взять ремень или веревку длиной в диаметр круга, сложить ее пополам и связать в кольцо; один конец получившейся петли накинуть на центральный кол, а в другой на полном натяжении петли вставить колышек, который и будет очерчивать по земле окружность. Далее остается только обойти вокруг центрального кола; петля же здесь нужна для того, чтобы ремень скользил по центральному колу, а не наворачивался на него — иначе получится спираль, а не окружность.

Однако значительное количество — практически половина — известных каменных кругов Европы имеют более сложную форму, чем окружность; в большинстве случаев это правильный эллипс — достаточно сложная замкнутая кривая, в простейшем случае вырождающаяся в окружность. Очевидно, что эллипсовидные каменные круги Европы не являются «ошибкой», допущенной при создании «круглых кругов»: во-первых, мы уже говорили о точности, с которой работали строители мегалитов; во-вторых, о каком отклонении от круга можно говорить, например, когда длина каменного эллипса вдвое превышает его ширину; и, наконец, речь ведь идет именно об эллипсе — вполне конкретной геометрической фигуре, — а вовсе не о произвольном овале. Иначе говоря, вытянутые каменные круги вытянуты намеренно и, более того, в соответствии с определенными математическими законами.

Мы уже упоминали тот факт, что большинство новгородских каменных кругов («молодых» по сравнению с британскими) также имеют вытянутую форму. Само по себе это, возможно, еще ни о чем не говорит, но вот то, что упомянутый выше круг у деревни Коломо представляет собой точный эллипс с фокальным расстоянием 4,17 м и эксцентриситетом 0,47, уже заставляет задуматься…

Впрочем, вернемся к вопросу о том, как наши предки вычерчивали на поверхности земли столь сложные кривые.

Итак, с кругом все просто: центральный кол и ременная (веревочная) петля, длина которой равна диаметру круга. Все просто рассчитать и просто — оставляя в стороне техническо-бытовые проблемы — реализовать.

С эллипсом все значительно сложнее. В рамках аналитической геометрии форма эллипса элементарно описывается в параметрическом виде, чуть сложнее — в полярных координатах, очень сложно — привычных декартовых. Но древние строители мегалитов, как мы уже упоминали, вряд ли владели высшей математикой; зато в их распоряжении были вторичные свойства кривых: так, например, описанный выше очевидный способ построения окружности основан на том, что окружность — это геометрическое место точек, равноудаленных от некоей точки, которая и является ее центром.

В отличие от окружности, эллипс определяется не одной точкой-центром, но двумя точками, которые называются его фокусами и лежат на главной (длинной) его оси. Уникальное свойство эллипса заключается в том, что сумма расстояний от любой его точки до фокуса-1 и до фокуса-2 неизменна. А поскольку расстояние между фокусами неизменно по определению, то это дает нам (и нашим предкам) способ построения эллипса на местности, минуя хитрости аналитической геометрии. Достаточно вбить в землю два столба, накинуть на них все ту же ременную петлю и обойти, удерживая петлю в натяжении, эти столбы вокруг: фигура, которую очертит на земле ввязанный в петлю колышек, и будет эллипсом!

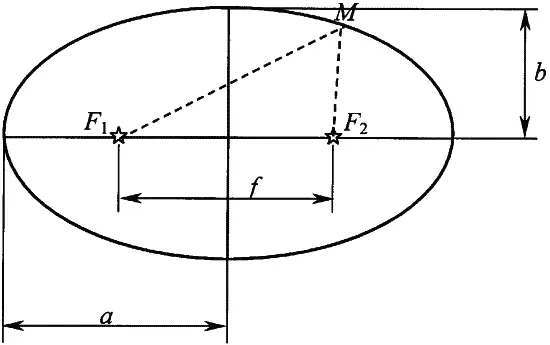
Просто? Отнюдь нет. Проблема заключается в том, что требуется-то не произвольный эллипс, а эллипс с более или менее заданными длиной и шириной (вряд ли каменные круги, на сооружение которых нередко уходили десятилетия, а то и века, создавались «просто так», наобум). Геометрическая задача: на каком расстоянии нужно расположить столбы-фокусы, чтобы получить, следуя вышеописанной технологии, эллипс с нужными длиной и шириной?

Сейчас эта задачка решается элементарно: несложно показать, что длина эллипса, его ширина и расстояние между фокусами связаны теоремой Пифагора, т. е.:

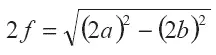
Определив таким образом расстояние между столбами, несложно посчитать и требуемую длину петли — она будет равна расстоянию между столбами плюс заданную длину каменного эллипса (говоря современным языком — удвоенной сумме фокального расстояния и большой полуоси эллипса).

Но все это легко в XXI веке, когда теорему Пифагора изучают едва не в начальных классах школы. Строители же мегалитов вряд ли владели теоремой Пифагора, какой бы простой она ни казалась нам. Что же оставалось им — очевидно, древнейший и многократно проверенный практикой путь эмпирики, путь «проб и ошибок». Иначе говоря, им требовалось опытным путем подобрать такое соотношение между длинами трех отрезков, чтобы, сложенные концами, они образовывали прямоугольный треугольник, — тогда его гипотенуза будет пропорциональна длине эллипса, один из катетов — ширине эллипса, а другой — искомому расстоянию между столбами. И уж конечно, таковое соотношение должно выражаться целыми числами — вряд ли тысячи лет назад строителям мегалитов было удобно работать с дробями…

…Природа, как сказал герой одного советского фантастического фильма, ставит перед нами труднейшие задачи, но она же всегда предлагает нам способ их разрешения. Дело в том, что существует так называемый простейший «пифагоров треугольник», являющийся прямоугольным при том, что длины его сторон пропорциональны небольшим целым числам: 3:4:5. Действительно, 3 2+ 4 2= 5 2. Кто знает, что было бы, если бы такого треугольника не существовало… Но он существует, и на его основе построена геометрия очень многих мегалитических сооружений Западной Европы; известный исследователь британских мегалитов Джон Вуд даже назвал его в этой связи «вездесущим треугольником 3:4:5». Существуют и другие пифагоровы треугольники (т. е. прямоугольные треугольники, соотношение сторон которых выражается целыми числами), например, треугольник 8:15:17 или 5:12:13; многие из них также обнаружены в геометрии мегалитических сооружений Западной Европы, и все-таки классический 3:4:5 встречается в мегалитах чаще всего.

Итак, что же нужно было древнему мастеру, чтобы построить «каменный эллипс» заданных размеров? Прежде всего — знать несколько пифагоровых треугольников (или хотя бы один, простейший) — наверняка это знание было сакрализовано и передавалось от учителя к ученику. Последовательность действий мастера должна была быть примерно такой (представим, что нам нужен эллипс длиной 10 метров и воспользуемся классическим треугольником 3:4:5):