Джозеф Фаррелл - Боевая машина Гизы

Эта неоднозначная связь между ε/π и √3/ 2привела Торрана к геометрии вписанного в сферу тетраэдра, позволившей разрешить эту неоднозначность. Синус угла 60° равняется √3/ 2, или 0,866025, а соотношение ε/π дает величину 0,865256, что приводит нас к тетраэдру. Причина этого заключается в том, что «площадь поверхности сферы, разделенная на площадь поверхности тетраэдра, дает очень точное приближение числа ε, которое мы обозначим как ε': ε = 2,718282, ε' = 2,720699». Подставляя ε' в соотношение ε/π, получаем результат 0,866025, практически совпадающий с √3/ 2. Это, по всей видимости, подтверждает выдвинутое в книге «Звезда Смерти Гизы» предположение, что основой гармонической унификации физики служили сконструированные геометрические аппроксимации фундаментальных констант.

На сайте Хогланда, тем не менее, приводится еще одна интересная геометрическая закономерность, на которой он подробно не задерживается. Если представить два тетраэдра, вписанные во вращающуюся сферу любого радиуса таким образом, что каждый тетраэдр ориентирован на противоположный полюс оси вращения и они перпендикулярны друг другу с точки зрения осевой симметрии, то получится знакомый символ священной геометрии, присутствующий в различных оккультных системах:

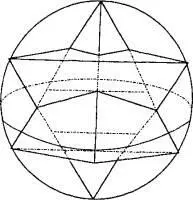
Этот символ представляет собой «звезду Давида», вавилонский знак, который евреи принесли с собой после возвращения из вавилонского плена и который с тех пор стал знаменитым символом иудаизма. Но возможно, это и самый известный символ совершенной физики, в чем мы вскоре убедимся.

Первое, что бросается в глаза, это его сходство с геометрией комплекса Гизы, повернутого вокруг оси, проходящей через вершину Великой пирамиды, о чем говорилось в главе IV:

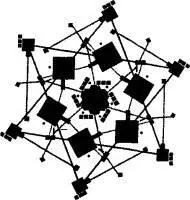
Это сходство, по всей видимости, подтверждает гипотезу Алана Элфорда, проанализированную в главе II — о том, что Вторая пирамида, Сфинкс, третья пирамида, а также «храмы» и «аллеи» были построены гораздо позже Великой пирамиды, но согласно точному геометрическому плану. То есть остальные крупные постройки могли быть возведены на старых местах, ранее занятых чем-то другим, или на тех местах, которые предусматривались первоначальным планом. В любом случае если рассматривать весь комплекс как единое целое, создается впечатление, что он намеренно был спланирован таким образом, чтобы вращать фундаментальную геометрию пространства. Таким образом, комплекс представляет собой двумерный аналог трехмерной фигуры из двух вписанных в сферу тетраэдров. Другими cловами, комплекс Гизы является масштабным образцом тех тетраэдрических физики и математики, которые Хогланд и Торран обнаружили в Сидонии на Марсе.

Это обстоятельство служит подтверждением еще одной гипотезы, выдвинутой Хогландом и другими исследователями: вполне возможно, что те, кто построил комплекс в Сидонии, возвел также Великую пирамиду и спланировал геометрию Гизы. В любом случае в основе этих сооружений лежит та же самая физика, и если Великая пирамида действительно представляла собой машину или оружие, то у нас появляется ключ к разгадке происхождения комплекса в Сидонии. А это, в свою очередь, согласуется с нашей гипотезой, что цивилизация, построившая Великую пирамиду, могла совершать межпланетные путешествия… и вести межпланетную войну.

Но что это за физика? Хогланд не дает пояснений ни к рисунку, ни к правильному шестиугольнику, образованному плоскостью пересечения двух тетраэдров, вписанных в сферу. Он утверждает, что геометрия вписанных тетраэдров является отражением нового источника энергии и на основе этого выдвигает предположения об особенностях планетарной и небесной механики, которые впоследствии подтвердились. Однако он необычно немногословен, когда речь заходит о том, почему эта геометрия воплощает новый источник энергии и что это за энергия. Я убежден, что его молчание объясняется тем, что он очень хорошо понимает, какие последствия будет иметь применение этой физики, а также ее военный потенциал. Мы можем лишь догадываться, что в действительности представляет собой физика вписанных тетраэдров.

Теперь следует вновь обратиться к векторному анализу, вектору трансляции и кватернионной геометрии и вспомнить, что в стандартном векторном анализе нулевая сумма векторной матрицы означает, что на приведенных ниже рисунках вектор трансляции равен нулю, несмотря на тот очевидный факт, что сама геометрия отражает разные внутренние вращения и напряжения.

Вспомним, что в векторном анализе сумма сил в обе-их приведенных выше простых геометрических фигурах равняется нулю — из-за отсутствия скалярной составляющей. Но в кватернионном анализе, где каждый вектор состоит из собственно вектора и скаляра (то есть чистой величины, без направления), сумма сил в этих фигурах существенно отличается — в шестщтольнике получается с\мма шести скалярных величин а 2+ Ь 2+ с 2+ d 2+ е 2+ f 2> О

Продолжим векторный анализ, обратив внимание, что каждая грань тетраэдра может представлять собой модель векторной системы с нулевой суммой, кватернионная сумма которой дает три скаляра. Разворачивая или «расплющивая» трехмерный тетраэдр в двухмерное изображение, мы получаем возможность увидеть, каким образом векторный анализ системы с нулевой суммой тем не менее указывает на точки напряжения, или потенциалы, причем именно там, где по мнению Хогланда, вращающиеся массы демонстрируют подобный апвеллинг энергии, то есть в точках 19,5° северной или южной широты.

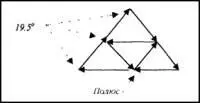
Теперь вернемся к рисунку вписанного в сферу тетраэдра и предположим, что каждое его ребро представляет собой вектор силы, а сам тетраэдр является пространственной геометрической фигурой с нулевой векторной суммой, то есть с отсутствующим вектором трансляции. Еще раз «расплющим» пространственную фигуру в двухмерное изображение, которое будет выглядеть следующим образом:

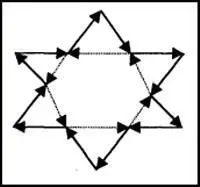
Здесь наглядно видно, как геометрия — с некоторым риском упрощения — моделирует две взаимосвязанные системы, каждая из которых в отдельности характеризуется нулевой векторной суммой. Общая векторная сумма этих систем тоже равна нулю, но скалярный потенциал в кватернионном анализе имеет очень большую величину, поскольку в нем каждый вектор включает скалярную составляющую, чистую магнитуду силы. Свернув нашу двухмерную модель в трехмерное изображение, мы получим приведенный выше чертеж. Обратите внимание на то, где проявляются точки напряжений при взаимодействии двух пространственных фигур.