Дэвид Шпигельхалтер - Искусство статистики. Как находить ответы в данных

В теоретической физике стандартом считается объявление об открытии в терминах «сигм», где результат «два сигма» означает наблюдение, которое на две стандартные ошибки отклонилось от нулевой гипотезы (вспомните, что мы использовали греческую букву сигма (σ) для обозначения среднеквадратичного отклонения в генеральной совокупности): «сигмы» в теоретической физике точно соответствуют t -значению в результатах работы компьютерной программы для множественной линейной регрессии, показанных в табл. 10.5. Наблюдение, которое в соответствии с критерием хи-квадрат давало двустороннее P-значение 1 на 3,5 миллиона, отличалось бы от нулевой гипотезы на пять стандартных ошибок. Поэтому об открытии бозона Хиггса объявили как о результате уровня пять сигма.

Команда из ЦЕРН не хотела объявлять о своем «открытии» до тех пор, пока P-значение не стало крайне малым. Во-первых, им нужно было учесть тот факт, что проверки значимости выполнялись для всех уровней энергии, а не только однократно в итоговой проверке по методу хи-квадрат – в физике такой эффект при многократном тестировании известен как Look-elsewhere effect [201]. Во-вторых, они хотели быть уверены, что любая попытка воспроизвести результат даст тот же вывод. Было бы слишком неловко делать ложные заявления о законах физики.

Что касается ответа на вопрос, поставленный в начале этого раздела, то сейчас разумнее предположить, что бозон Хиггса существует. Это утверждение становится новой нулевой гипотезой, пока, возможно, не появится более глубокая теория.

Теория Неймана – Пирсона

Почему для исследования по защите сердца понадобилось больше 20 тысяч участников?

Исследование по защите сердца было масштабным, но его размер не определялся произвольным образом. При планировании испытания исследователи должны были указать, сколько людей нужно включить в группу, употребляющую статины или плацебо, причем требовалось серьезное статистическое обоснование, чтобы оправдать стоимость такого эксперимента. План опирался на идеи, развитые Ежи Нейманом и Эгоном Пирсоном, которых мы уже упоминали как разработчиков понятия доверительных интервалов.

Идею P-значений и проверок значимости Рональд Фишер внедрил в 1920-х годах как способ проверки разумности какой-то конкретной гипотезы. Если наблюдается маленькое P-значение, то либо случилось нечто удивительное, либо нулевая гипотеза ложна: чем меньше P-значение, тем обоснованнее утверждение, что она неверна. Эта методика задумывалась как довольно неформальная процедура, но разработанная Нейманом и Пирсоном в 1930-х теория индуктивного поведенияпопыталась поставить ее на более строгий математический фундамент.

Конструкция ученых требовала указывать не только нулевую, но и альтернативную гипотезу, которая предоставляла более сложное объяснение данных. Затем они рассматривали возможные решения после проверки – либо отвергнуть нулевую гипотезу в пользу альтернативы, либо не отвергать [202]. Это приводило к вероятности появления двух видов ошибок – ошибки первого рода, возникающей, когда мы отклоняем истинную нулевую гипотезу, и ошибки второго рода – когда принимаем неверную нулевую гипотезу. Строгая юридическая аналогия проиллюстрирована в табл. 10.6: ошибка первого рода – это осудить невиновного человека, а ошибка второго рода – признать кого-то невиновным, тогда как на самом деле он совершил преступление.

Таблица 10.6

Возможные результаты проверки гипотезы, по аналогии с судебным разбирательством

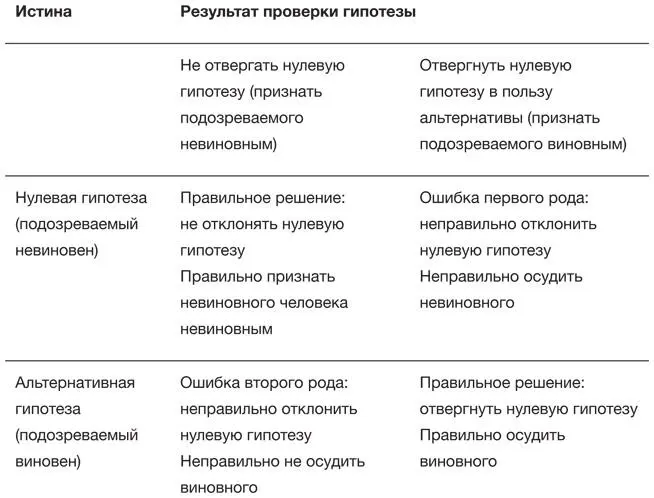
Нейман и Пирсон предложили при планировании эксперимента выбирать две величины, которые вместе определяют, насколько масштабным он должен быть. Во-первых, следует заранее зафиксировать значение для вероятности ошибки первого рода (при условии, что нулевая гипотеза верна), скажем 0,05; это называется размером критерияи, как правило, обозначается буквой α (альфа). Во-вторых, нужно заранее определить вероятность ошибки второго рода (при условии, что альтернативная гипотеза верна); она традиционно обозначается β (бета). На самом деле исследователи обычно работают с величиной 1 – β, которая именуется мощностью критерияи представляет собой вероятность отклонить нулевую гипотезу в пользу альтернативной, когда последняя верна. Другими словами, мощность в каком-нибудь эксперименте – это вероятность, что будет правильно обнаружен реальный эффект.

Налицо тесная связь между размером α и P-значением Фишера. Если в качестве пороговой величины, при которой результаты считаются значимыми, взять число α, то результаты, которые заставят нас отказаться от нулевой гипотезы, будут в точности теми же, для которых P < α. Поэтому α можно рассматривать как пороговый уровень значимости: α = 0,05 означает, что мы отвергнем нулевую гипотезу для всех P-значений меньше 0,05.

Существуют формулы для размера и мощности при различных видах экспериментов, и каждая зависит от размера выборки. Но если у выборки фиксированный размер, то компромисс неизбежен: чтобы увеличить мощность, мы можем ослабить порог для «значимости» и тем самым с большей вероятностью идентифицировать истинный эффект, однако это означает увеличение вероятности ошибки первого рода (размера). В юридической аналогии мы можем ослабить критерии для осуждения (например, снизив требования для стандарта доказывания «вне разумных сомнений»), что в результате приведет к большему количеству правильно осужденных преступников, но, увы, и к большему количеству невинно осужденных.

Теория Неймана – Пирсона берет начало в процессах контроля качества на производстве, но в настоящее время широко используется при проверке новых методов лечения. Перед началом рандомизированного клинического исследования в протоколе указывается нулевая (лечение неэффективно) и альтернативная (как правило, эффект одновременно правдоподобен и важен) гипотезы. Затем исследователи устанавливают размер и мощность критерия, нередко выбирая α = 0,05 и 1 – β = 0,80. Это означает, что для объявления результата значимым организаторы эксперимента требуют, чтобы P-значение было меньше 0,05, и с 80-процентной вероятностью достигнут этого, если лечение на самом деле эффективно. Вместе эти два числа позволяют оценить необходимое количество участников эксперимента.

Если исследователи хотят провести какое-то определяющее клиническое испытание, им нужно быть строже. Например, исследование по защите сердца пришло к выводу, что

если холестериноснижающая терапия за 5 лет сокращает смертность от сердечно-сосудистых заболеваний примерно на 25 %, а смертность от всех причин – на 15 %, то исследование именно такого размера имеет прекрасные шансы для демонстрации подобных эффектов на убедительных уровнях статистической значимости (то есть мощность > 90 %, p < 0,01).