Ласло Мерё - Логика чудес. Осмысление событий редких, очень редких и редких до невозможности

Разумеется, на рост могут влиять не только генетические компоненты, но и факторы окружающей среды. На рост нашего тела влияют несколько генов, и все они сравнительно слабые. Кроме того, действуют внешние факторы — например, питание в детстве. В упрощенной модели дело обстоит похожим образом и с уровнем интеллектуального развития, хотя для него выявлено еще меньше генетических факторов, а факторы воздействия окружающей среды тоже очень разнообразны — от уровня питания ребенка до того, как ему читают и как с ним разговаривают. Никому не достаются только те факторы, что вносят свой вклад в более высокое интеллектуальное развитие, но те, кому их достается больше, предположительно получают более высокий уровень интеллекта.

Этот результат тоже в точности соответствует тому, что моделирует доска Гальтона. Разумеется, биологические явления гораздо сложнее, чем эта простая машина. События, влияющие на то, в каком месте в конце концов окажется шарик, — отскоки влево и отскоки вправо — независимы друг от друга. Шарик отскакивает на некотором уровне влево или вправо независимо от того, влево или вправо он отскочил на предыдущем. Эта независимость и позволяет машине приблизиться к распределению Гаусса.

В биологических системах такая независимость встречается редко. Каждый из факторов, влияющих на определенную характеристику, будь то ген, воздействие среды или что-то еще, обычно не бывает независимым от других факторов. Более того, разные факторы обычно влияют на получающуюся характеристику в разной степени. Поэтому на самом деле доска Гальтона моделирует мир живых существ лишь в очень ограниченных пределах.

Нельзя сказать, чтобы математики приняли все это как данность. Многие типы центральной предельной теоремы были доказаны, причем было продемонстрировано, что разные варианты биномиального распределения также стремятся к распределению Гаусса. Например, было показано, что компоненты, вносящие свой вклад в некоторую характеристику, могут быть неодинаковой силы. На некоторых уровнях доски Гальтона они могут отскакивать вправо или влево не на один столбец, а на два или три. Такой сценарий труднее осуществить физически, но математический результат остается неизменным: в конце концов фасолины, попавшие в пазы, располагаются в соответствии с распределением Гаусса. Кроме того, события на том или ином уровне не обязательно должны быть независимы от другого уровня. Например, на поведение шарика на каком-то уровне до некоторой степени может влиять то, как он отскочил от шпенька уровнем раньше. До сих пор появляются все новые варианты центральной предельной теоремы. Суммарную картину, полученную на основе нескольких вариантов центральной предельной теоремы, можно приблизительно резюмировать следующим образом:

Если некая характеристика определяется несколькими слабыми компонентами («слабыми» в том смысле, что ни один из них не сильнее всех других)

и между этими компонентами нет сильной взаимозависимости (то есть нет таких нескольких компонентов, которые определяют значения всех остальных),

то такая характеристика должна быть распределена по всей популяции в соответствии с распределением Гаусса.

Эту картину точно иллюстрирует представленное на илл. 7 распределение значений коэффициента интеллектуального развития (IQ). Оно очень похоже на гауссиану, которую мы видели раньше, за исключением небольшой «шишечки» в районе 70, единственного нарушения плавной картины. Эта «шишечка» соответствует популяции больных синдромом Дауна.

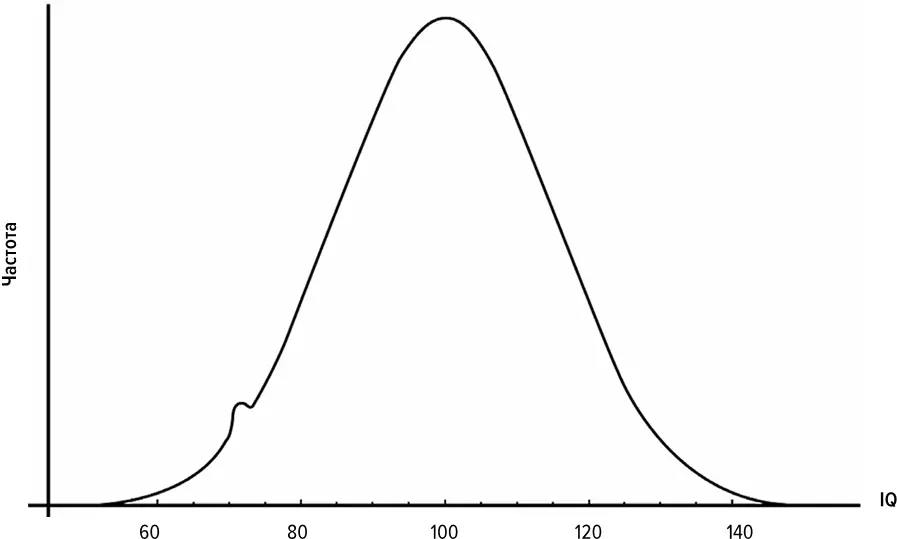
Илл. 7.Распределение значений IQ

(График Йожефа Бенце, на основе данных Kun and Szakács, 1997)

Синдром Дауна — это генетическое заболевание, вызванное наличием лишней копии 21-й хромосомы. Воздействие лишней хромосомы на уровень интеллектуального развития более или менее подавляет эффект всех остальных факторов — не настолько, чтобы человек полностью утрачивал все интеллектуальные способности, но у большинства взрослых с синдромом Дауна IQ бывает между 50 и 70, и все другие факторы, определяющие интеллектуальное развитие, влияют на эту цифру очень слабо. В случае интеллектуального развития другие столь же подавляющие компоненты появляются настолько редко, что их воздействие не отражается на кривой распределения (синдром Дауна встречается приблизительно у одного из тысячи новорожденных).

Рост распределяется примерно так же. Поскольку существует несколько генетических компонентов, которые неизбежно вызывают необычайно низкий или высокий рост, на кривой распределения роста, по форме весьма близкой к гауссиане, есть несколько пиков. В то же время с массой тела дело обстоит иначе. В следующей главе мы узнаем, почему это так.

Математика центральной предельной теоремы образует фундамент, на котором природа может строить стабильные конструкции — например, популяции живых организмов. Возможно, пока природа экспериментировала по всей Вселенной, пробуя то одно, то другое, она создавала структуры как стабильные, так и нестабильные. По определению, выжили именно первые. Судя по тому, что мы знаем о физике, которая формировала космос после Большого взрыва, и о законах биологической эволюции, действенный способ достижения стабильности заключается в создании такой системы, в которой определенная характеристика создается сочетанием нескольких более или менее независимых компонентов сравнимой силы. Именно такое сочетание гарантирует, что данная характеристика будет распределена по приблизительно нормальному закону, что, в свою очередь, гарантирует ее стабильность из поколения в поколение (если не происходит резких изменений условий окружающей среды).

Однако несмотря на все усилия природы — а может быть, просто в соответствии с природой вещей, — иногда ей не удается создать характеристику через взаимодействие множества слабых компонентов. Иногда, как в случае синдрома Дауна, возникает компонент, подавляющий все остальные. Но даже в случае появления такого компонента природа применяет уловку — формирует каждую важную характеристику из суммы нескольких мелких, более или менее независимых компонентов, — и этого, как правило, бывает достаточно для достижения стабильности.

Я не знаю, что на самом деле является руководящим принципом природы — стремление к стабильности или просто сборка всего на свете из множества мелких компонентов, порождающая стабильность в качестве побочного продукта самого принципа строительства. Как бы то ни было, именно из-за центральной предельной теоремы столь многое в природе действует в соответствии с законами Тихонии и повсюду не царит свойственная Диконии нестабильность. Как мы помним из разговора о распределении Коши, положение точки, в которой выстрел Фиби попадает в стену, определяется одним-единственным компонентом, а именно тем угловым положением относительно стены, в котором Фиби оказывается после разворота. Если она повернута почти параллельно стене, малейшее изменение угла дает огромное расхождение в результатах. Поэтому нас не должно удивлять, что результат этот получается диконским — нестабильным в традиционном смысле этого слова. В Тихонии, где явления порождаются взаимодействием многочисленных мелких компонентов, мы ожидаем стабильности, с четко определенными понятиями среднего, или математического ожидания, и стандартного отклонения от среднего. Но в Диконии нормальна только ненормальность. Возможно все, что угодно, и у событий нет стандартного отклонения.