Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

Это позиционная система счисления, в которой любое число можно представить с помощью всего двух цифр: 0 и 1. Чтобы преобразовать двоичное число в десятичное, нужно заменить все единицы степенями двойки. Показатели этих степеней будут зависеть от позиции цифры: правый разряд соответствует 2 0, следующий — 2 1и так далее. Например, двоичное число 110101 в десятичной системе выглядит так: 1 • 2 0+ 0 • 2 1+ 1 • 2 2+ 0 • 2 3+ 1 • 2 4+ 1 • 2 5= 1 + 4 + 16 + 32 = 53.

Аналогично для записи десятичного числа в двоичном виде нужно разделить его на 2, полученный результат снова разделить на 2 и так далее до тех пор, пока результатом деления не будет 1. Последний результат деления будет первой цифрой справа. Все прочие остатки отделения, от последнего к первому, составят следующие разряды (остаток от деления на 2 может равняться только 0 или 1). Например, 39 в двоичной системе записывается как 100111, так как 39:2 дает 19 (и остаток 1), 19:2 дает 9 (остаток 1), 9:2 дает 4 (остаток 1), 4:2 дает 2 (остаток 0), 2:2 дает 1 (остаток 0). Мы выразили число в виде суммы степеней двойки.

Итак, 39 =1 + 2 + 4 + 32 = 1•2 0+1•2 1+1•2 2+0•2 3+0•2 4+1•2 5= 100111 по основанию 2. Хотя двоичная нотация появилась сравнительно недавно, свойство, на котором она основана («всякое число можно представить в виде суммы различных степеней двойки»), было известно и применялось еще в древности. Например, древние египтяне использовали для умножения такую систему. Один из сомножителей удваивался, второй делился на 2. Если число было нечетным, то на 2 делилось предыдущее число. Этот метод дает верный результат именно благодаря указанному свойству.

Страница бюллетеня Французской академии наук, посвященная двоичной системе счисления, разработанной Лейбницем в 1703 году.

Вращаем кубик. Это стратегическая игра для двух игроков. Первый игрок ставит кубик на стол выбранной стороной вверх. Второй игрок поворачивает кубик на четверть оборота так, что на верхней грани будет уже другое число очков, и прибавляет это число к первому. Затем каждый игрок по очереди вращает кубик на четверть оборота (так можно получить любое число, кроме тех, что расположены на верхней или нижней грани кубика) и прибавляет число очков на верхней грани к общей сумме. Тот, кто набирает в сумме 31, выигрывает.

Какой из игроков имеет преимущество? Как нужно играть, чтобы всегда выигрывать?

Разрезаем прямоугольник. Это стратегическая игра для двух игроков. На листе бумаги в клетку нужно нарисовать прямоугольник размерами 17 × 15 клеток. Затем нужно пометить квадратик в нижнем правом углу. Каждый из игроков своим ходом делит прямоугольник на две части вертикальной или горизонтальной линией и удаляет ту часть прямоугольника, которая не содержит маленький отмеченный квадрат. Тот, кто не сможет разделить прямоугольник (то есть от прямоугольника останется только один отмеченный квадратик), проигрывает.

Какой из игроков имеет преимущество? Как нужно играть, чтобы всегда выигрывать?

Пересекаем круг.Это стратегическая игра для двух игроков. На листе бумаги нужно нарисовать окружность и обозначить на ней восемь произвольных точек. На каждом ходу игрок соединяет две точки отрезком. Он может соединить любые две точки, кроме уже соединенных, но нарисованный им отрезок не должен пересекать никакой другой отрезок. Игрок, которому не удастся провести такой отрезок, проигрывает.

Какой из игроков имеет преимущество? Что изменится, если изменить начальное число точек?

При анализе целей и правил игры можно увидеть, что во многих случаях на первый взгляд отличающиеся стратегические игры на самом деле эквивалентны. И напротив, очень похожие игры в действительности сильно отличаются друг от друга и выигрышные стратегии для них явно разнятся.

Игровое поле изображено на рисунке 1. Каждый игрок берет единственную фишку, которая изначально расположена в ячейке S, и передвигает ее на соседнюю клетку. При этом он всегда должен двигаться вправо — по горизонтали или по диагонали. Игрок, который поставит фишку в крайнюю клетку М, выигрывает.

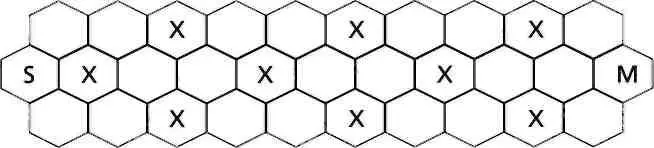
Рисунок 1.

Если читатель попытается решить игру сам, то легко увидит, в какие клетки нужно ставить фишку, чтобы победить. Если рассуждать в обратном направлении, то станет понятно, что первый игрок будет всегда выигрывать, если будет ставить фишку в помеченные крестиком клетки. Совсем не очевидно, что эта игра аналогична игре 1 («выигрывает первый»), если не заметить, что допустимые ходы можно интерпретировать как переход на два шага вперед (если мы передвигаем фишку в горизонтальном ряду) или на один шаг вперед (если мы двигаем фишку по диагонали и переставляем ее в другой ряд). Если пронумеровать клетки таким способом, то станет четко видна аналогия между этими играми (рисунок 2).

Рисунок 2.

На игровой доске всего один ряд из шести клеток. На нем расставлены три фишки. На каждом ходу игрок выбирает фишку и передвигает ее вправо на любое количество клеток (минимум на одну и максимум на пять, в крайнюю правую клетку). Цель игры — поставить все фишки в крайнюю правую клетку. Тот, кто ставит в эту клетку последнюю фишку, выигрывает. В одной клетке могут одновременно находиться несколько фишек. Заметим, что эта игра эквивалентна первой рассмотренной нами версии игры Ним (игра 4): каждая фишка соответствует кучке, перенос фишки вправо соответствует взятию фишек из кучки в игре Ним. Когда фишка попадает в крайнюю правую клетку, это равносильно тому, что из кучки в игре Ним взяты все фишки. Рассмотрим еще две игры и проанализируем их эквивалентность.

На стол выкладываются две кучки фишек, например 7 и 5 фишек. Каждый игрок может брать из выбранной кучки любое число фишек (минимум одну). Он также может брать фишки из двух кучек сразу, но в этом случае нужно брать одинаковое число фишек из каждой кучки.

На одну из клеток шахматной доски, например клетку h8, ставится ферзь. Каждый игрок может передвигать ферзя на любое количество клеток влево, вниз или по диагонали (то есть одновременно влево и вниз). Тот, кто поставит ферзя в клетку a1, то есть в левую нижнюю клетку, выигрывает.