Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

В кооперативных играх решением называется альянс и соответствующее распределение платежей, которые будут стабильны, то есть будут гарантировать согласие всех членов коалиции.

Допустим, что в прошлом примере предприниматели решили разделить прибыль согласно сделанным вложениям. Таким образом, Анна имеет 5 голосов, Борис — 3, Василий — 1 голос. Теперь большинство могут получить следующие коалиции: АБВ, АБ, АВ, А.

Анна имеет большинство, поэтому она может присвоить все деньги себе: А = 200000 евро, Б = 0 и В = 0. Распределение будет несправедливым, но стабильным. Анна согласна с таким решением, а образовать альянс без нее невозможно. Следовательно, приведенное решение удовлетворяет всем необходимым условиям, которые мы определили выше.

В подобных играх ценой игры называется платеж, который гарантирован каждому игроку, если тот будет действовать рационально, и не зависит от решений остальных участников. В примере 1 никому из них не гарантирована какая-либо сумма. Следовательно, ценой игры будет А = 0, Б = 0 и В = 0. Напротив, во втором примере ценой игры будет А = 200 000, Б = 0 и В = 0.

Усложним ситуацию еще больше, чтобы сделать ее более реальной. По результатам выборов 81 кресло в парламенте было распределено между пятью партиями следующим образом: А = 33, Б = 24, В = 15, Г = 6, Д = 3. Ни одна из партий не имеет абсолютного большинства (41 кресло), и для формирования правительства необходимо образовать коалицию. Эта коалиция займется распределением бюджетов и установит нужные обязанности. Партии имеют схожую идеологию, и предполагается, что мера ответственности определяется подконтрольным бюджетом. Кроме того, предполагается, что никто не будет нарушать процедуру голосования.

Из всех возможных альянсов (1 из пяти партий, 5 из четырех, 10 из трех, 10 из двух и 5 из одной) нам важны лишь 16 (они будут иметь минимум 41 кресло в парламенте). Так как ни одна партия не имеет большинства, цена игры для каждой партии равна 0, так как ни одна из партий не должна обязательно входить в состав коалиции, которая сформирует новое правительство.

Этот американский математик и экономист внес фундаментальный вклад в теорию игр. Он изучал математику в Гарвардском университете, откуда выпустился в 1948 году после службы в армии и участия во Второй мировой войне в звании сержанта. Затем он в течение года работал в корпорации RAND и в 1953 году получил степень доктора в Принстонском университете, где в то время работали создатели теории игр. Затем он вернулся в RAND, где проработал до 1981 года, после чего занял должность профессора в Калифорнийском университете (UCLA). Уже в своей докторской диссертации он ввел некоторые значимые понятия теории игр, например вектор Шепли. На протяжении всей своей долгой научной деятельности он публиковал и продолжает публиковать исследования по этой тематике. Является членом Национальной академии наук США с 1979 года. Лауреат множества премий, среди которых премия фон Неймана (1981).

Для подобных ситуаций экономист и математик Ллойд Шепли предложил распределение, пропорциональное числу возможных выигрышных коалиций, в которых данный игрок имеет определяющую роль (без него альянс не наберет нужного числа голосов). Платеж, получаемый каждым игроком, называется значением Шепли. Игрок не играет определяющую роль в коалиции, если его участие не обязательно для победы этой коалиции.

В нашем примере в альянсе, образованном всеми пятью партиями, ни одна из них не играет определяющую роль. Например, в коалиции БВГД партии Б и В играют определяющую роль: без их участия коалиция не наберет большинство (без партии Б коалиция будет иметь лишь 24 места, без партии В — 33). Напротив, Г и Д не играют определяющей роли: если одна из этих партий покинет коалицию, та сохранит большинство (без партии Г коалиции будет принадлежать 42 кресла, без партии Д — 45). Число коалиций, в которых определяющую роль играют те или иные партии, представлено в таблице ниже

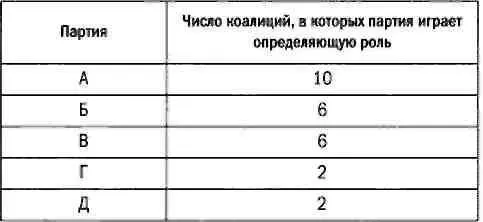
Теперь мы можем распределить бюджет согласно модели Шепли. Допустим, что коалиция образована всеми партиями, и в их распоряжении находится бюджет в размере 2,6 млрд евро. Распределение по модели Шепли (в миллионах евро) выглядит так:

А = 1000,

Б = 600,

В = 600,

Г = 200,

Д = 200.

В любом другом альянсе каждая партия-участник получит часть общего бюджета согласно этим же правилам, и полученная сумма никогда не будет меньше полученной в составе этой коалиции. Это не единственное стабильное распределение, но для любой коалиции распределение, выполненное подобным образом, будет наиболее стабильным, и не будет способа, при котором суммы платежей для участников коалиции будут больше.

Метод фон Неймана, равно как и метод Шепли, показывает следующее: с одной стороны, решением является не единственное распределение, а множество распределений; с другой стороны, мы можем найти множество характеристик, которые помогут понять, является ли данное распределение частью «решения» или нет.

По прочтении двух последних глав читатель заметил, что чем сложнее анализируемые ситуации (и в то же время чем они ближе к реальности), тем менее категоричны математические методы, используемые при решении. Это не означает, что какое-то решение будет более корректным, чем другое. Это значит, что реальные ситуации, в которых сочетается сотрудничество и соперничество, обладают индивидуальными отличительными свойствами. Поэтому в применяемых математических методах нужно учитывать, что их корректность будет зависеть от данных конкретных свойств.

Comas, О., El mundo en juegos, Barcelona, RBA, 2005.

Corbalan, F., Juegos matematicos para secundaria у bachillerato, Segunda edition, Madrid, Sfntesis, 1998.

Davis, M.D., Introduction a la teoria de juegos, Col. Ensayo, Madrid, Alianza, 1998. DEULOFEU, J., Una recreation matematica: historias, juegos у problemas, Barcelona, Planeta, 2001.

—: Gimnasia mental 2, Madrid, Martinez Roca, 2003.

Gardner, M., Matematicas para divertirset Barcelona, RBA, 2007.

Lucas, E., Recreaciones matematicas, 4 vols, Madrid, Nivola, 2007-2008.

Mlllan, A., GlORGIO, I., El mundo сото un juego matematico. John von Neumann un tientifico del siglo XX, Madrid, Nivola, 2001.

Packel, E., Las matematicas de los juegos de apuestas, Col. La Tortuga de Aquiles 5, Madrid, DLS-EULER, 1995.

Poundstone, W., El dilema del prisionero. John von Neumann, la teoria de juegos у la bomba, Coleccion Ciencia у Tecnica, Madrid, Alianza, 2005.

Steen, L.A. у otros, Las matematicas en la vida cotidiana, Madrid, Addison-Wesley/ Universidad Autonoma de Madrid, 2006.