Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

В 2001 году режиссер Рон Ховард снял фильм «Игры разума», удостоенный четырех «Оскаров», в котором рассказывается о жизни Джона Нэша и в особенности о его борьбе с шизофренией, от которой он страдал на протяжении многих лет.

Примеры из предыдущего раздела показывают, что в играх с нулевой суммой иногда можно использовать стратегии сотрудничества, которые позволяют улучшить результат. Проблемы возникают, когда новый результат не распределяется между игроками поровну. Иными словами, стоит вопрос о том, как распределить «излишки» и довольны ли игроки рациональным распределением этих «излишков».

Меррил Флад, в свое время работавший в RAND, проанализировал различные ситуации из повседневной жизни, особенно те, в которых игрокам требовалось распределить между собой дополнительный выигрыш. Одна из таких ситуаций — продажа подержанного автомобиля. Допустим, покупатель готов купить машину у друга, который, в свою очередь, готов ее продать. Чтобы узнать стоимость машины, друзья отправляются в автомагазин, который согласен приобрести автомобиль за 1000 долларов и продать за 1300 долларов, получив минимум 300 долларов за свои услуги. Если продажа будет совершена без участия магазина, очевидно, что друзья сэкономят 300 долларов и смогут разделить эту сумму между собой. В этом случае наиболее рационально разделить эту сумму пополам, то есть продать машину за 1150 долларов. Таким образом, каждый из друзей получит по 150 долларов.

Это решение рационально, но не единственно. Один из игроков, например покупатель, может решить, что не готов платить больше 1100 долларов, то есть продавец получит 100 долларов в дополнение к установленной цене. И наоборот, продавец может установить минимальную цену в 1250 долларов, аргументируя это тем, что покупатель все равно сэкономит 50 долларов. Заметим, что если покупатель не примет предложение продавца, рационально рассудив, что выгода разделена «несправедливо», то повредит сам себе, потому что установленная цена все равно будет ниже цены магазина.

Однако мысль о «справедливом» распределении выгоды не всегда столь очевидна. Иногда может существовать несколько решений, которые будут казаться полностью обоснованными. Допустим, Михаил хочет отправиться из Барселоны в Мадрид (600 км) на машине, чтобы посетить важное совещание и вернуться на следующий день. Он узнает, что Петр, его друг, который живет в Сарагосе, тоже должен поехать в Мадрид в этот же день. Друзья решают вместе поехать на машине и туда, и обратно. Как нужно распределить расходы на поездку, учитывая, что Сарагоса расположена на полпути между Барселоной и Мадридом?

Вариант 1. Так как Михаил проедет в два раза больше, чем Петр, расходы нужно разделить на 3, Петр заплатит одну треть, Михаил — две трети.

Вариант 2. Так как Михаил проедет в одиночку половину пути, а другую половину друзья проедут вместе, то Михаил оплатит расходы за половину дороги плюс еще одну четверть, а оставшаяся четверть расходов (половина половины) придется на долю Петра. Получается, что расходы нужно разделить на 4, Петр оплатит одну четверть, Михаил — три четверти.

Чтобы подсчитать расходы на поездку, предположим, что поездка из Барселоны в Мадрид обойдется Михаилу в 600 евро (если он поедет один), а поездка из Сарагосы в Мадрид обойдется Петру в 300 евро. Если они поедут вместе, то сэкономят 300 евро. В первом варианте Михаил платит 400 евро (экономит 200), Петр платит 200 евро (экономит 100). Во втором варианте Михаил платит 450 евро (экономит 150), Петр платит 150 евро (также экономит 150). Получается, что во втором варианте выгода распределяется одинаково, а в первом распределение происходит пропорционально понесенным расходам. Таким образом, в конкретной ситуации может существовать несколько разумных и обоснованных решений.

Игра под названием дилемма заключенного (этот термин был предложен Альбертом Такером в 1950 году) принадлежит к числу наиболее известных задач теории игр. Это простой пример того, как две противоборствующие стороны могут соперничать или сотрудничать. Подобное встречается очень часто: в ценовых войнах, рекламных кампаниях или в гонке вооружений.

В традиционной формулировке речь идет о противостоянии двух преступников, каждый из которых может хранить молчание или свидетельствовать против другого. Однако мы рассмотрим эту дилемму на интересном практическом примере военного конфликта, которые, к сожалению, до сих пор слишком часто происходят в разных уголках планеты. Дилемма будет формулироваться так:

Две противоборствующие стороны Р1 и Р2 должны определить политику в области вооружений. Каждая из сторон может независимо от другой выбрать одну из двух стратегий:

А: отказаться сотрудничать, то есть вооружиться перед возможным военным конфликтом.

Б: сотрудничать, то есть разоружаться или наложить ограничение на некоторые виды оружия.

Такер внес важный вклад в топологию, нелинейное программирование и теорию игр. Он окончил Торонтский университет с дипломом по математике, затем защитил докторскую в Принстонском университете в 1932 году. Некоторое время он работал в Гарварде, Кембридже и Чикаго, затем вернулся в Принстон, где преподавал до 1970 года, свыше 20 лет возглавляя кафедру математики. В 1950 году он дал название самому известному и интересному парадоксу в теории игр — дилемме заключенного, а также впервые привел интерпретацию зтой задачи. Тем самым он внес фундаментальный вклад в модель соперничества и сотрудничества, над которой позднее работали Меррил Флад и Мелвин Дрешер в Принстонском университете.

Он был не только выдающимся исследователем, но и видным преподавателем, принимал участие в образовательных проектах для средней школы, за что был избран президентом Математической ассоциации Америки. Среди его учеников — нобелевский лауреат Джон Нэш.

Существует четыре возможных решения: (А, А), (А, Б), (Б, А) и (Б, Б). Первая координата в каждой паре — стратегия Р1, вторая — стратегия Р2. Возможные исходы можно представить таблицей:

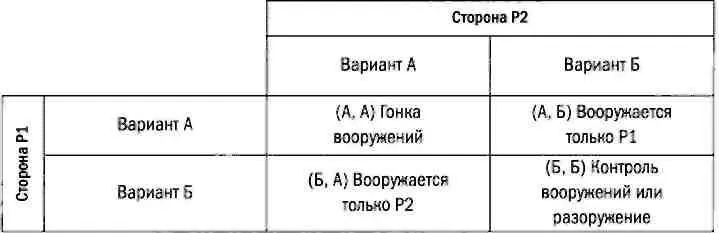
Пересечениям возможных стратегий можно присвоить значения (в терминах теории игр — платежи), учитывая, что для каждого игрока они будут отличаться и в каждой ячейке будет два числа: одно означает выгоду Р1, второе — выгоду Р2. Получим следующую платежную матрицу: