Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

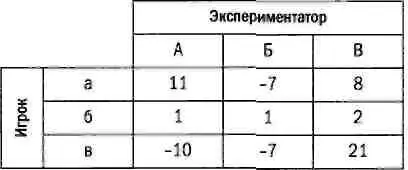
Игру можно быстро решить с помощью теоремы о минимаксе. Точка равновесия — элемент матрицы (б, Б), равновесное значение равно 1. Следовательно, игрок всегда должен выбирать стратегию б, экспериментатор — стратегию Б, и в каждой партии выигрыш игрока будет равен 1.

Опыты показали, что игроки применяли стратегию б, когда видели, что экспериментатор всегда придерживается стратегии Б. Напротив, когда экспериментатор действовал случайным образом, они меняли стратегию и обычно применяли вариант а, чтобы получить максимальный выигрыш, осознавая при этом возможность проигрыша. Последующие опросы показали, что более половины игроков считали, что систематическое следование стратегии Б со стороны экспериментатора «глупо», так как он соглашался с проигрышем в 1. Если бы он применял другие стратегии, то, «возможно», мог бы улучшить свой результат. Игроки не обратили внимания, что если бы они следовали стратегии б, то экспериментатору был бы гарантирован проигрыш минимум в 1.

Этот и другие похожие эксперименты показали, что разумные действия, направленные на увеличение выигрыша, встречаются не всегда. Люди предпочитают стратегии, которые, как кажется, приносят больший выигрыш. Лишь после того, как они несколько раз убедятся в обратном, они приходят к оптимальной стратегии. Если же в игре нет седловой точки и нужно применять смешанные стратегии, то реальное поведение игроков еще сложнее. В этом случае игрокам был известен алгоритм решения, но, несмотря на это, больше половины не стали утруждать себя вычислениями и действовали интуитивно. Как правило, их действия отличались от оптимальной смешанной стратегии.

Все подобные эксперименты показывают, что в реальных ситуациях нужно ставить под сомнение «разумные» предположения о том, что, например, соперник будет действовать оптимальным образом и в соответствии со своими интересами. Возможно, объяснение кроется в том, что минимаксная стратегия является защитной: она гарантирует результат, который будет оптимальным, когда соперник будет действовать разумно. Однако почему игрок не будет стараться получить больше гарантированного минимума?

В этой главе мы проанализировали игры с нулевой суммой и пришли к выводу: в играх такого типа существует оптимальная стратегия для каждого игрока, а также цена игры, которая позволяет определить средний выигрыш каждого. Исходные данные подобных игр всегда можно представить в виде так называемой платежной матрицы. В ней строки соответствуют стратегиям первого игрока, столбцы — стратегиям второго игрока. Вкратце игры для двух игроков с нулевой суммой решаются следующим способом.

Нужно вычислить максиминное значение (максимальное из минимальных) для первого игрока и минимаксное (минимальное из максимальных) для второго. Если эти значения совпадают, то оптимальные стратегии для обоих игроков имеют одинаковый результат (он называется ценой игры), и игра решена. В этом случае стратегии называются чистыми.

Если же максиминное и минимаксное значения не совпадают, нужно отложить в сторону чистые стратегии (с помощью которых определялись минимаксное и максиминное значения) и рассмотреть все чистые стратегии для каждого игрока, присвоив каждой стратегии определенную вероятность. Эти вероятности (их сумма будет равна 1) определят оптимальную смешанную стратегию и позволят рассчитать среднюю цену игры для каждого игрока.

Определение вероятностей и средней цены для каждого игрока осуществляется решением системы линейных уравнений (число уравнений зависит от количества стратегий), где неизвестными являются искомые вероятности и средняя цена игры. Если средняя цена для обоих игроков совпадает, то игра решена, и вероятности, найденные для каждого игрока, определяют его оптимальную стратегию, которая будет смешанной (так как в ней будет присутствовать элемент случайности).

Если найденные средние цены игры отличаются либо если одна из вероятностей оказалась отрицательной, то игра не решена. В этом случае ее нужно проанализировать снова, чтобы определить, возможно ли найти какую-либо доминантную стратегию. Если это невозможно, то описанный нами метод неприменим.

Во всех задачах, представленных в прошлой главе, речь шла о соперничестве: выигрыш одного игрока всегда равнялся проигрышу другого, поэтому подобные игры называются играми с нулевой суммой. Это конфликтные ситуации, участники которых имеют прямо противоположные цели. Каждый игрок стремится получить максимальный выигрыш, что будет означать максимальный проигрыш соперника.

В этой главе мы рассмотрим немного другую тему. Целью игроков по-прежнему будет выигрыш, все так же будет существовать конфликтная ситуация, но это еще не все. С одной стороны, выигрыш одного не обязательно будет соответствовать проигрышу другого, и будут существовать стратегии, в которых выиграть могут оба игрока. С другой стороны, будут существовать ситуации, в которых сотрудничество будет выгодным для обеих сторон. Таким образом, в играх возникают коммуникация и взаимное доверие, но также и угрозы, цель которых — заставить соперника выполнить обещанное. В этих случаях речь идет о не полностью конфликтных ситуациях, и мы будем различать кооперативные и некооперативные стратегии .

Вспомним, что теория игр изучает принятие решений. В настоящей главе этому аспекту уделено особое внимание, так как во многих ситуациях, о которых мы расскажем далее, будет присутствовать выбор между соперничеством и сотрудничеством. Какие решения будут принимать игроки в этих условиях? Подобные ситуации порождают так называемые дилеммы , так как оба игрока могут соперничать или сотрудничать друг с другом, и неясно, какой вариант окажется более выгодным, поскольку все будет зависеть от решения, принятого оппонентом. В целом сотрудничество игроков принесет выгоду обоим, и результат будет наилучшим для каждого из игроков, в то время как соперничество приведет к печальным последствиям. Если бы существовали лишь две эти ситуации, то дилеммы бы не было. Однако если один из игроков пытается сотрудничать с другим, а тот решает соперничать, последний будет иметь преимущество, причем оно будет больше, чем при сотрудничестве. Таким образом, дилемма очевидна.