Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

Средний доход можно было вычислить напрямую с помощью формулы V = (ad - bc) / (а + d - b - с), где a, b, с, d — элементы платежной матрицы (слева направо и сверху вниз). Для данной задачи получим (500 • 900 - 300 • 100)/(500 + 900 - 300 - 100) = 420000/1000 = 420, что очевидно совпадает с результатом, полученным выше из системы линейных уравнений.

С другой стороны, мы действовали так, как если бы экономическая обстановка определялась некоей смешанной стратегией. Аналогичные расчеты показывают, что вероятность хорошей экономической обстановки равна 2/5, следовательно, вероятность плохой экономической обстановки равна 3/5.

Пенальти в футболе можно рассматривать как антагонистическую игру между пенальтистом и вратарем, где интересы участников прямо противоположны. Допустим, что пенальтист может пробить вправо, влево или по центру (это три чистые стратегии), а вратарь может прыгнуть в правый или левый от себя угол или же остаться в центре ворот (это также три чистые стратегии). На основании статистики была сформирована следующая таблица:

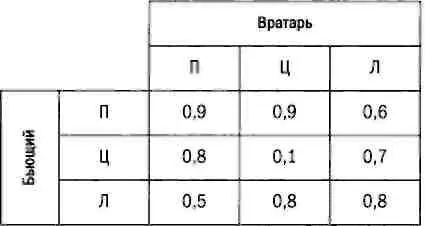
Элементы матрицы означают вероятность гола (то есть выигрыш бьющего) в зависимости от стратегии, выбранной обоими игроками. Например, если пенальтист бьет вправо, а вратарь прыгает в правый от себя угол, вероятность гола равна 0,9. Если же удар придется по центру и вратарь останется стоять в центре, то вероятность гола будет равной всего 0,1. Какой стратегии должны придерживаться бьющий и вратарь?

Корпорация RAND (от англ. Research and Development — «Исследования и разработка») — американский исследовательский центр, созданный после Второй мировой войны с целью проведения стратегических исследований для военно-воздушных сил США. Многие проекты корпорации были засекречены и не доведены до логического завершения, но нет никаких сомнений, что в RAND работали одни из лучших ученых в области теории игр. В 1948 году Центр получил статус частной организации, работающей исключительно на военно-воздушные силы, которые полностью его финансировали. Именно в этой корпорации были проведены фундаментальные исследования, которые способствовали развитию теории игр.

Внутренняя организация Центра больше напоминала научно-исследовательский институт, чем военное учреждение. В 50-е и 60-е годы прошлого века помимо прикладных исследований, связанных с ядерным оружием и началом холодной войны, в корпорации также проводились фундаментальные исследования силами выдающихся математиков и экономистов. Среди них все тот же Джон фон Нейман, Джон Нэш, Меррил Флад, Кеннет Эрроу и многие другие ученые, расцвет деятельности которых пришелся на этот короткий промежуток времени, совпавший с началом бурного роста теории игр.

Новая штаб-квартира корпорации RAND в Санта-Монике, Калифорния.

Первоначальный анализ показывает, что не существует доминантной чистой стратегии и что задача не имеет решения в чистых стратегиях, так как максиминное значение равно 0,6, а минимаксное — 0,8. Иными словами, пенальтист ожидает забить 6 из 10 пенальти, а вратарь ожидает, что пропустит гол в 8 из 10 случаев. Оба хотят (и могут) улучшить свой результат (т. е. выигрыш): пенальтист хочет, чтобы вероятность забить была выше 0,6, а вратарь хочет, чтобы вероятность пропустить была ниже 0,8.

Рассчитаем оптимальную смешанную стратегию для бьющего и для вратаря, а также среднюю цену игры, которая будет означать среднюю вероятность того, что с пенальти будет забит гол. В этом случае средняя цена игры будет лежать в интервале от 0,6 до 0,8.

Чтобы определить оптимальную смешанную стратегию для бьющего, нужно рассчитать вероятности выбора каждой из трех чистых стратегий. Обозначим их p( правый угол), p( левый угол), p( центр). Так как p( правый угол) + p( левый угол) + p( центр) = 1, число переменных можно сократить до двух: p( правый угол), p( центр), 1 - p( правый угол) - p( центр). Ожидаемую цену игры обозначим за V.

Если вратарь прыгнет в правый от себя угол, то ожидаемый выигрыш пенальтиста составит

V = 0,9 p( правый угол) + 0,8 p( центр) + 0,5 (1 - p( правый угол) - p( центр)).

Если вратарь останется в центре, то

V = 0,9 p( правый угол) + 0,1 p( центр) + 0,8 (1 - p( правый угол) - p( центр)).

Если же вратарь прыгнет в левый от себя угол, то

V = 0,6 p( правый угол) + 0,7 p( центр) + 0,8 (1 - p( правый угол) - p( центр)).

Мы получили систему из трех линейных уравнений. Ее решением будет являться p( правый угол) = 0,37; p( центр) = 0,19; p( левый угол) = 1 - p( правый угол) - p( центр) = 0,44. Цена игры для бьющего равна V = 0,71.

Аналогично можно рассчитать вероятности для каждой из трех чистых стратегий вратаря, но эту задачу мы оставляем читателю.

Несомненно, теорема о минимаксе и метод, показанный в прошлых разделах, как для чистых, так и для смешанных стратегий, — это мощные инструменты для решения матричных игр и определения оптимальных результатов. Эта теорема применяется в экономике, политике, спорте и военном деле. С ее помощью были решены не только задачи, в которых имеются доминантные стратегии или седловая точка, но также задачи без седловой точки, в которых можно определить среднюю цену игры, оптимальную для обеих сторон, и необходимые смешанные стратегии.

Несмотря на это, во всех случаях мы предполагали, что выполняется одно условие: игроки действуют «разумно». Иными словами, каждый игрок считает, что его соперник всегда действует в своих интересах и использует стратегию, оптимальную с этой точки зрения. Но что происходит, если это не так и если один из игроков пытается обмануть оппонента?

Мортон Дэвис во введении в теорию игр рассказывает о различных исследованиях, которые проводились в 1950—1970-е годы. Целью исследований было наблюдение за поведением реальных игроков в матричных играх. Так, в 1964 году Ричард Брейер придумал игру, разрешимую в чистых стратегиях, то есть в этой игре было легко найти точку равновесия. Игрокам говорили, что против них в одних случаях будет играть опытный игрок, в других — игрок, который будет действовать случайным образом. В действительности игроки всегда играли против экспериментатора, который менял стратегию: иногда он следовал оптимальной стратегии Б, иногда действовал случайным образом. Платежная матрица этой игры выглядела так: