Карл Левитин - Геометрическая рапсодия
- Название:Геометрическая рапсодия
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:1984
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Карл Левитин - Геометрическая рапсодия краткое содержание
Плоское и объемное, свойства кристаллов и правильных тел, симметрия, замкнутость и бесконечность Вселенной — эти темы-мелодии сливаются в книге в некий гимн во славу Геометрии.
Для иллюстрирования книги использованы гравюры голландского графика М. К. Эсхера, геометрические по своему содержанию.
Научно-художественная книга для широкого круга читателей.
Геометрическая рапсодия - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Но если считать — хотя это было бы большой ошибкой — все эти работы чисто геометрическим юмором, то двум последним шуткам предшествовало несколько более плоских острот. Плоских — в прямом смысле этого слова.
В июне 1936 года читатели журнала "Нейчур" были приятно удивлены. Известнейший английский химик Фредерик Содди, который получил Нобелевскую премию за то, что открыл изотопы, на этот раз порадовал ученый мир поэмой, состоящей из трех стансов. Она называлась (в вольном переводе) "Поцелуй по расчету", и первый ее станс звучал приблизительно так:
Когда к устам прильнут уста,
Быть может голова пуста.
Но если вдруг четыре круга
Решат поцеловать друг друга,
То лишь геометра расчет
Их к поцелую приведет.
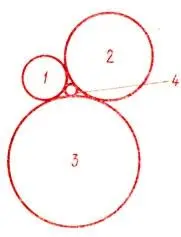
Вариантов два, любой не плох:
Все три в одном, один средь трех (1) [2] Здесь, а также далее, в скобках стоят номера рисунков, гравюр, фотографий и чертежей, которые, если взглянуть на них, порой могут доставить несколько секунд удовольствия, не говоря уже о том, что они имеют прямое отношение к тексту.
.
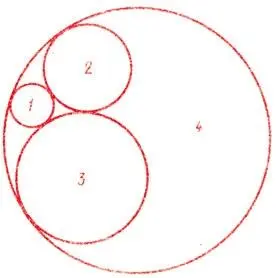
Коль три в одном, то изнутри
К гиганту тянутся они. (2).
Но и средь трех он рад вполне:
Три поцелуя — все извне.
В следующем стансе Содди в том же поэтическом ключе сообщает придуманную им формулу: удвоенная сумма квадратов обратных радиусов равна квадрату их суммы.
В этой несложной формуле Содди предусмотрел и тот случай, когда больший круг охватывает три меньших: тогда надо просто брать величину радиуса со знаком "минус". Всякому ясно, что теперь ничего не стоит вычислить радиус четвертого круга, чтобы он смог "поцеловаться" с тремя другими.
Впоследствии выяснилось, что формулу эту знал еще Рене Декарт. Но Содди открыл ее вполне самостоятельно. И кроме того, он не удовлетворился целующимися кругами. В третьей и последней части своего "Поцелуя по расчету" Содди перешел с плоскости в пространство от кругов к сферам. И тут прежде всего обнаружилось, что в целовальном обряде принимают участие не четыре, а пять сфер, а чтобы они могли коснуться друг друга, им надо, говоря презренной прозой, подчиниться требованиям формулы: утроенная сумма квадратов обратных радиусов равна квадрату их суммы.
Любители математических головоломок приуныли: все загадки о соприкасающихся кругах и сферах стали решаться с удручающей легкостью. Ну вот, к примеру, одна из них, просто так, чтобы лишний раз помянуть добром Содди. На столе лежат три арбуза, каждый диаметром в тридцать сантиметров, а под ними — апельсин. Конечно же, все фрукты, выращенные в садах геометрии, имеют идеальную сферическую форму. А потому легкий вопрос: каков диаметр апельсина?
Но Нобелевский комитет не дал Фредерику Содди еще одну премию, быть может, потому, что его формулы никак не помогали решать другие геометрические задачи, которые отняли у мыслящего человечества не одну тысячу человеко-часов. А именно — "упаковочные" головоломки. Формулируя задачу на теперь уже привычном нам языке геометрической эротики, мы поставим вопрос так: каково максимальное число кругов (или сфер), которые могут одновременно поцеловать один (одну) такой (такую) же, целуясь при этом со своими соседями?
На плоскости задача элементарно проста: шесть кругов касаются седьмого, центрального (3). (В качестве таких кругов приятно взять четыре гравюры М. К. Эсхера, которые называются "Пределы на круге".) Но со сферами дело обстоит куда сложнее — недаром Ньютон так и не смог убедить своего друга Грегори, что их может быть не больше тринадцати, включая сюда и "целуемую".
В те годы пинг-понг еще не был в моде, а то бы спорщики могли поставить любопытный эксперимент. Отбросив предрассудок, им надо было взять "чертову дюжину" шариков и сдавить их прозрачной резиновой пленкой. Они могли бы убедиться, что "обычная" дюжина охватывает "чертов" шарик таким образом, что все двенадцать шариков располагаются в вершинах воображаемого икосаэдра (правильного двадцатигранника) и между ними остается небольшой зазор (4). Но достаточен ли этот зазор, чтобы втиснуть еще и четырнадцатый шарик? Вот в чем вопрос. Можно пробовать располагать шары в самых различных комбинациях, но место для еще одного не освобождается. Это, однако, вовсе не доказывает, что такую удачную комбинацию найти невозможно.
Но все-таки — да или нет? Как доказать строго? Хоппе придумал — думайте, если это доставляет удовольствие, и вы.

Быть может, подобные головоломки вам, как и Исааку Ньютону, покажутся трудными, но попытайтесь все-таки совершить над собой некое интеллектуальное насилие. Все это не просто стандартные "вопросы на повторение пройденного". Впереди космическое развитие темы Круга и Сферы, и к нему надо подготовиться.
1
...По счастью, журнал "Нейчур", заложивший основы изучения геометрических поцелуев, известен своей серьезностью. Серьезностью даже в шутках. Напечатав стансы Содди о целующихся кругах и сферах, редакция посчитала, что вопрос освещен недостаточно фундаментально. И спустя полгода, в январском номере 1937 года, опубликовала еще один заключительный станс, принадлежащий перу Форольда Госсета, обитавшего отнюдь не на Парнасе, но в Кембриджском университете. Это было одно из многих стихотворных произведений, присланных в редакцию с единственной целью: обобщить формулу Содди на случай n-мерного пространства, в котором целуются, естественно, n-мерные сферы — гиперсферы.
Чтобы вполне насладиться этим поэтическим шедевром, нам надо справиться с совсем простым делом: представить в себе n-мерную сферу.
2
"Когда нематематик слышит о четырехмерных вещах, его охватывает священный трепет..." — так говорил Альберт Эйнштейн. А Герман фон Гельмгольц считал, что представить себе четвертое измерение — все равно что слепому от рождения вообразить краски. Заметьте, речь идет всего лишь о четвертом измерении. Что же тогда сказать о пятом, шестом, а то и вообще об n-м?
И все-таки рискнем!
Впервые слова "n-мерное пространство" прозвучали в 1854 году в речи Бернгарда Римана при вступлении его на должность преподавателя Геттингенского университета. Она называлась "О гипотезах, образующих основания геометрии" и в самом деле провозглашала совсем новую, неожиданную и уж во всяком случае неевклидовую геометрию, названную впоследствии "римановой". Впрочем, и Евклид, создавая свою геометрию, возможно, размышлял о "мере мира". "Точка — это то, что не имеет частей", — говорил он. Современный математик посчитал бы эти слова пусть примитивным, но довольно точным определением "объекта нулевого измерения". Точка, оставленная карандашом на бумаге, острие булавки или башенного шпиля — вот эти "объекты" в реальной жизни. Сфера нулевого измерения — это и есть точка.
Читать дальшеИнтервал:
Закладка:





