Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Леонардо родился в Италии и вырос на севере Африки, где его отец Гильермо трудился дипломатом, обеспечивая мирную торговлю с Беджаей (современным Алжиром). Сопровождая отца в деловых поездках, мальчик быстро усвоил арабскую систему записи чисел и оценил ее значение. В 1202 г. в своей «Книге абака» он пишет: «Когда отец мой был назначен на должность таможенного чиновника, заведовавшего в Беджае делами стекавшихся к нему пизанских торговцев, он в отрочестве моем призвал меня к себе и предложил несколько дней учиться счетному искусству, сулившему немало удобств и выгод для моего будущего. Наученный благодаря мастерству учителей основам индийского счета, я приобрел большую любовь к этому искусству».

Его книга открывает для Европы индийско-арабский способ записи чисел и содержит почти все арифметические и алгебраические сведения того времени, изложенные исключительно полно и глубоко, а также дает примеры решения практических задач, в частности связанных с торговлей. И хотя прошло еще несколько веков, пока индийско-арабские символы окончательно вытеснили из обихода привычный абак, преимущества этой стройной системы записи и подсчетов вскоре стали очевидны.

Леонардо также известен под прозвищем Фибоначчи (от Filius Bonacci, или «сын Боначчи»), но это имя не появлялось в письменных трудах до XVIII в. Псевдоним был дан ему позже, предположительно Гийомом Либри.

Мы не так часто прибегаем на практике к обыкновенным дробям. Гораздо чаще используются десятичные: например, π = 3,14159 – не точно, но вполне достаточно для большинства подсчетов. Стоило бы сделать рывок к десятичным дробям, но мы договорились следовать за идеей, а не хронологией, и придется перейти к дальнейшим фактам. Итак, переносимся в 1585 г., когда Вильгельм Оранский избрал фламандца Симона Стевина советником своего сына Морица, графа Нассауского.

Воспользовавшись возможностью, Стевин сумел сделать хорошую карьеру, став инспектором водных сооружений, главным военным квартирмейстером и под конец – министром финансов. Он быстро осознал необходимость в точных процедурах бухгалтерского учета и обратился к итальянским математикам эпохи Возрождения, а также к переложению для Европы индийско-арабской системы счисления, сделанному Леонардо Пизанским. Он находил вычисления при помощи простых дробей громоздкими и неудобными и предпочел бы более точную и аккуратную систему, предложенную вавилонянами, – если бы в ее основании не находилось число 60. Стевин попытался найти вариант, сочетавший лучшие черты подходов, и изобрел десятеричный аналог вавилонской системы – десятичные дроби.

Стевин опубликовал арифметику десятичных дробей, а также пылкую и аргументированную статью о полезности их применения: «Все необходимые для делопроизводства вычисления можно будет делать с помощью целых чисел, без добавления дробей».

В его системе еще не использовалась знакомая нам запятая, но она очень скоро приняла современный вид. Там, где мы бы написали 5,7731, Стевин писал 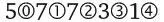. Символ 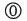обозначал целое число, 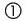– одну десятую, – одну сотую и т. д. Привыкнув к этой системе, люди вскоре отказались от символов , и т. д., оставив только , который сократился и упростился до обычной запятой.

Математики все числа, употребляемые при счете, называют натуральными . Добавив к ним отрицательные числа, мы получим множество целых чисел. Рациональные числа – положительные и отрицательные дроби, вещественные числа (действительные) – положительные и отрицательные десятичные дроби со сколь угодно большим числом цифр после запятой.

Как же отрицательные числа вошли в историю?

На заре первого тысячелетия в Китае вместо абака пользовались системой счетных палочек. Чтобы изображать числа, их выкладывали группами.

Верхний ряд на картинке показывает вертикальные палочки, представляющие единицы, сотни, десятки тысяч и т. д., соответствовавшие их положению в ряду символов. Нижний – горизонтальные палочки, представляющие десятки, тысячи и т. д. Здесь мы имеем два чередующихся типа. Подсчеты велись с помощью обоих типов палочек.

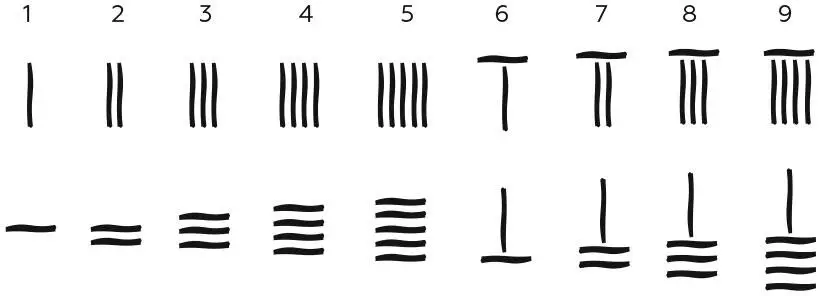
Счетные палочки древних китайцев

Для решения системы двух линейных уравнений китайские математики должны были разложить палочки на столе. Они использовали красные для чисел, которые собирались прибавлять, и черные – для вычитания. И тогда для решения системы уравнений, которую мы бы записали так:

3 x – 2 y = 4

x + 5 y = 7,

они бы выложили в виде двух колонок на столе: одно с числами 3 (красные), 2 (черные), 4 (красные) и другое – 1 (красная), 5 (красные), 7 (красные).

Красно-черная система обозначения не приводит нас к отрицательным числам, это пока всего лишь операция вычитания. Однако она уже близка к самой «чжэн фу шу» – концепции положительных и отрицательных чисел. Здесь отрицательное число представлялось с использованием того же набора палочек, что и для положительных, с дополнительной отметкой в виде косой палочки над цифрой.

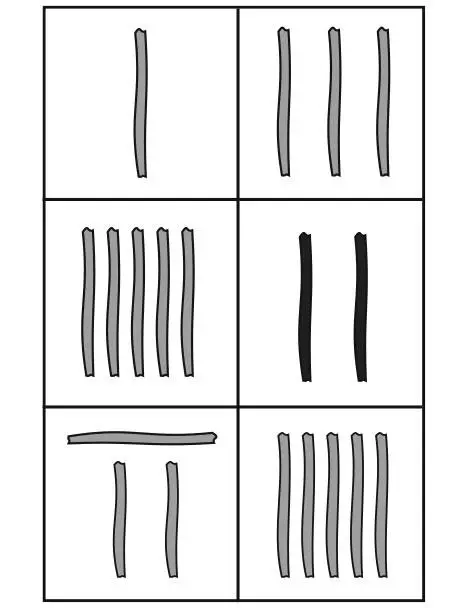
Уравнения в китайском стиле. Серыми изображены красные палочки

Согласно Диофанту, все числа могут быть только положительными. Он отвергал возможность существования отрицательных решений для уравнений. Но индийские математики считали отрицательные числа очень удобными для обозначения долгов в финансовых подсчетах: задолжать кому-то некоторую сумму в финансовом смысле считалось худшим вариантом, чем вообще не иметь денег. Ясно, что долг должен быть меньше 0. Если у вас было три фунта, а вы заплатили два, то у вас осталось 3–2 = 1 фунт. Иными словами, если у вас был долг два фунта, а вы получили три, ваша чистая прибыль составляет –2 + 3 = 1. Бхаскара замечает, что если конкретная задача имеет два решения, 50 и –5, то второе его категорически не устраивает: «Его не следует учитывать, потому что люди не приемлют отрицательных решений».