Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

θ = A sin kt + B cos kt

для констант A и B , определяющих начальное положение и угловую скорость маятника.

Этот подход имеет ряд преимуществ: например, мы можем легко определить, что период колебаний маятника – время, необходимое на его полное движение, – равен 2π/ k . Главный недостаток с точки зрения математики в том, что решение делается неверным, когда θ становится достаточно большим (и здесь большим окажется даже угол в 20°, если мы хотим получить точный ответ). Тут уже возникает вопрос строгости: имеем ли мы тут случай, когда точное решение для приблизительного уравнения не противоречит приблизительному решению для точного? Ответ положительный, однако это удалось доказать только в 1900 г.

Второе уравнение можно решить точно, потому что оно линейное – содержит только первую степень неизвестной θ и ее производную, а коэффициенты – константы. Функция, которая является прототипом решения для всех линейных уравнений, – экспонента y = e x. Она удовлетворяет уравнению:

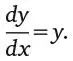
Таким образом, e x – собственная производная. Это свойство – одна из причин того, что логарифмы именно по основанию е принимаются как натуральные. Соответственно производная натурального логарифма ln x равна 1/ x , а интеграл от 1/ x равен ln x . Любое линейное дифференциальное уравнение с постоянными коэффициентами может быть решено с использованием экспоненциальных и тригонометрических функций (последние, как мы уже видели, на самом деле являются экспоненциальными, только замаскированы).

Различают два типа дифференциальных уравнений. Обыкновенные дифференциальные уравнения (ОДУ) имеют дело с неизвестной функцией y от одной переменной х , а также с различными производными от y , такими как dy / dx или d 2 y / d 2 x . До сих пор приведенные здесь примеры дифференциальных уравнений относились к обыкновенным. Гораздо более сложной, но и более важной для математической физики является идея дифференциальных уравнений в частных производных (ДУЧП). Это уравнения, содержащие неизвестные функции от двух и более переменных, таких как f ( x, y, t ), где x и y – координаты на плоскости, а t – время. ДУЧП содержат эту функцию в выражении с частными производными относительно каждой переменной. Новое выражение используется для описания производных от одних переменных с учетом других, а все остальные остаются неизменными. Таким образом, ∂ x /∂ t показывает скорость изменения x во времени, а y остается константой. Это называется частной производной, отсюда и термин «дифференциальные уравнения в частных производных».

Эйлер представил ДУЧП на суд ученых в 1734 г., а д’Аламбер опубликовал ряд работ по ним в 1743 г., но большинство ранних исследований проходило за закрытыми дверями. Первый большой прорыв случился в 1746 г., когда д’Аламбер вернулся к старой проблеме – колебаниям струны. Иоганн Бернулли обсуждал численный метод конечных элементов в 1727 г., учитывая колебания конечного числа точечных масс, расположенных равноудаленно друг от друга вдоль невесомой струны. Д’Аламбер рассматривает непрерывную струну с однородной плотностью, применяя вычисления Бернулли для n масс и предполагая, что число n стремится к бесконечности. Таким образом, непрерывная струна рассматривалась как бесконечное множество бесконечно малых сегментов, соединенных вместе.

Исходя из результатов Бернулли, основанных на открытом Ньютоном законе движения, и сделав некоторые упрощения (например, что размер колебаний небольшой), д’Аламбер пришел к формуле ДУЧП:

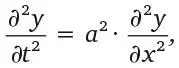
где y = y ( x, t ) описывает форму струны в момент времени t как функцию горизонтальной координаты x . Здесь a – константа, определяемая по натяжению и плотности струны. В продолжение научного спора д’Аламбер доказал, что общее решение для ДУЧП имеет вид:

y ( x, t ) = f ( x + at ) + f ( x – at ),

где f периодична, причем период вдвое длиннее струны, и f – нечетная функция, т. е. f (– z ) = – f ( z ). Эта формула удовлетворяет естественному граничному условию, что концы струны неподвижны.

Сегодня мы называем ДУЧП д’Аламбера волновым уравнением и интерпретируем его решение как суперпозицию симметрично расположенных волн, из которых одна движется со скоростью а , а вторая со скоростью – а (они перемещаются в противоположных направлениях). Это стало одним из самых важных уравнений в математической физике, потому что в природе волны встречаются повсюду, причем самые разные.

Эйлер ознакомился с работой д’Аламбера и тут же постарался улучшить ее. В 1753 г. он показал, что без граничных условий общее решение будет выглядеть так:

y ( x, t ) = f ( x + at ) + g ( x – at ),

где f и g периодичны, но не удовлетворяют никаким другим условиям. В частности, эти функции могут иметь различные формулы для разных областей x – особенность, которую Эйлер считал свойством функций, имеющих разрывы, хотя в современной терминологии они непрерывны, но имеют разрывную первую производную.

В более ранних работах, опубликованных в 1749 г., он указывал, что (для простоты мы принимаем, что длина струны равна единице) простейшие нечетные периодические функции являются тригонометрическими:

f ( x ) = sin x , sin 2 x , sin 3 x , sin 4 x …

и т. д. Эти функции представляют простые синусоидальные колебания с частотой 1, 2, 3, 4 и т. д. Эйлер утверждал, что общим решением здесь является наложение (суперпозиция) таких кривых. Базовая синусоида sin x является основной модой колебаний, а остальные будут более высокими модами, – в итоге получается то, что мы теперь называем гармониками.

Сравнение решений волнового уравнения, предложенных Эйлером и д’Аламбером, привело к фундаментальному кризису.

Д’Аламбер не признал возможности существования разрывных функций в интерпретации Эйлера. Более того, рассуждения Эйлера грешили одной нестыковкой, поскольку тригонометрические функции всегда непрерывны, и, следовательно, конечны наложения (суперпозиции) из них. Эйлер предпочел не углубляться в это противоречие между конечными и бесконечными суперпозициями. Впрочем, в те дни никто не был очень строгим в подобного рода вопросах и никто из ученых еще не ступил на этот сложный путь важности обоснования новых методов. Однако в итоге такое упущение привело к серьезным проблемам. На время разногласия утихли, пока новая работа Фурье не подлила масла в огонь.