Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

В 1807 г. Жозеф Фурье представил свой доклад о путях распространения тепла Французской академии наук, но его не утвердили из-за серьезных недоработок. Чтобы подтолкнуть ученого к дальнейшим исследованиям, Академия даже учредила к 1812 г. Большую премию за изучение теплопроводности. Поскольку о награде стало известно заранее, Фурье уже в 1811 г. успел оформить свои идеи в виде доклада на соискание премии и выиграл ее. Но его труд всё равно жестоко критиковали за недостаток логической строгости, и Академия не разрешила его публиковать в виде научной статьи. Фурье, в ярости из-за такого отношения, написал труд «Аналитическая теория тепла», изданный в 1822 г. Туда почти полностью и без изменений вошел доклад 1811 г., но было и много новых материалов. Наконец в 1824 г. ученого оценили по заслугам: он был избран секретарем Академии и уже без помех опубликовал в виде научной статьи свой доклад от 1811 г.

Первым шагом Фурье был вывод ДУЧП для описания теплопроводности. Там имелось множество упрощений и допущений: тело должно быть однородным (с одинаковыми свойствами по всему объему) и изотропным (его свойства не зависят от направления) и т. д. В итоге он получил выражение, которое теперь известно как уравнение теплопроводности. Оно описывает распределение температуры в любой точке трехмерного тела и в зависимости от времени. Уравнение теплопроводности очень похоже с виду на уравнение Лапласа и на волновое уравнение, но с частной производной по времени в первой степени, а не во второй. Это небольшое отличие очень важно для математики ДУЧП в целом.

Были выведены такие же уравнения для одномерных и двумерных тел (стержень и плоскость), полученные удалением переменной z (для двумерного тела) и y (для одномерного). Фурье решил уравнение теплопроводности для стержня (чью длину мы принимаем равной π), на концах которого сохраняется неизменная температура, с условием, что в момент времени t = 0 (начальное состояние) температура в точке x стержня принимает вид:

b 1sin x + b 2sin 2 x + b 3sin 3 x + …

(выражение, полученное с помощью предварительных вычислений), и сделал вывод, что температуру должно описывать схожее, но более сложное выражение, где каждый член умножается на соответствующую экспоненциальную функцию. Аналогия с гармониками в волновом уравнении поразительна. Но там каждая мода задана обычной синусоидой, колеблется бесконечно с одинаковой амплитудой, а здесь каждая синусоидальная мода распределения температуры убывает экспоненциально по времени, и более высокие моды убывают быстрее.

Типичный пример разрывной функции – прямоугольная волна S ( x ), которая принимает значение 1, когда −π < x ≤ 0, и равна −1, когда 0 < x ≤ π, и имеет период 2π. Применив формулу Фурье к прямоугольной волне, мы получаем ряд S ( x ) = sin x + 1/ 3sin 3 x + 1/ 5sin 5 x + …

Синусоиды складываются, как мы видим на схеме ниже.

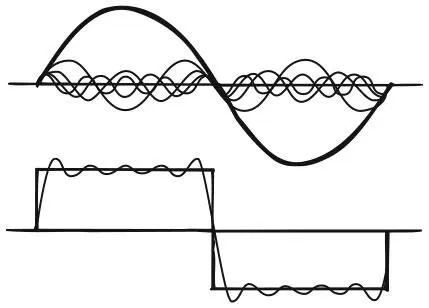
Представление с помощью ряда Фурье прямоугольной волны: вверху ее компоненты, синусоиды, внизу – их сумма

Хотя волна прямоугольной формы разрывная, каждое ее приближение будет непрерывно. Но по мере добавления всё б о льших членов ряда колебания растут, делая график рядов Фурье всё более крутым около точек разрыва. Здесь мы видим, как бесконечный ряд непрерывных функций может превратиться в разрывную функцию.

Причина такого различия в том, что в волновом уравнении энергия сохраняется, и поэтому колебание не затухает. А в уравнении теплопроводности тепло распространяется по всему стержню и теряется на его концах, потому что они охлаждаются.

Результатом работы Фурье стало то, что мы можем разложить начальное распределение температуры в ряд Фурье – сумму синусов и косинусов, похожую на приведенную выше формулу, а значит, способны немедленно описать, как тепло распространяется по телу со временем. Фурье считал очевидным, что такое выражение можно составить для любого начального распределения температуры, – и здесь-то начинались его неприятности. Мало кому из современников ученого было интересно, какое отношение теплопроводность имеет к волнам. Ее изучение казалось гораздо более сложным занятием.

Доводы Фурье в пользу возможности разложить функцию на синусы и косинусы были слишком сложными, запутанными и недостаточно строгими. Ему пришлось воспользоваться всеми разделами математики, чтобы в конце концов получить простые выражения для коэффициентов b 1, b 2, b 3и т. д. Обозначив начальное распределение температуры как f ( x ), он получил:

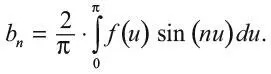
В 1777 г. Эйлер уже вывел эту формулу во время работы над волновым уравнением для звука и доказал ее с помощью мудрого наблюдения, заметив, что разные моды, sin m π x и sin n π x , являются ортогональными, т. е.

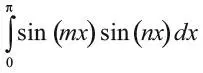
равен 0, если m и n – разные целые числа, не равные 0, т. е. на самом деле равен π/2, если m = n . Если предположить, что f ( x ) можно разложить в ряд Фурье, то, умножив обе стороны выражения на sin nx и проинтегрировав, мы избавимся от всех слагаемых, кроме одного, и в остатке получим формулу Фурье для b n.

Ни одно обсуждение ДУЧП в математической физике не будет полным без упоминания гидродинамики. И правда, эта область очень важна для практического применения, поскольку уравнения описывают, как вода обтекает подводные лодки или воздух – воздушные суда, и даже показывают сопротивление воздуха во время гонок «Формулы-1».

Эйлер сделал первые шаги в этой области в 1757 г., выведя ДУЧП для движения жидкости с нулевой вязкостью («липкостью»). Это уравнение остается в силе для некоторых жидкостей, но из-за излишней упрощенности не очень практично. Уравнения для вязких жидкостей вывел в 1821 г. Клод Навье, а потом их получил в 1829 г. Пуассон. Уравнения включают различные частные производные скорости движения жидкости. В 1845 г. Джордж Стокс вывел те же уравнения исходя из базовых физических принципов, и в итоге они получили название уравнения Навье – Стокса .

Предложенная Кеплером модель эллиптических орбит была не так точна. Она была бы надежной в случае двух тел в Солнечной системе, но уже появление третьего начинает менять (нарушать) эллиптическую орбиту. Огромные расстояния между планетами несколько смягчают это воздействие, отчего большинство орбит всё же остаются близкими к эллипсам. Но Юпитер и Сатурн ведут себя очень странно: то замедляются и не попадают вовремя в ожидаемую точку, то, наоборот, делают рывок вперед, опережая график. Этот эффект возникает из-за их взаимного притяжения, а также из-за притяжения к Солнцу.