Мартин Гарднер - Этот правый, левый мир

Маленьких детей обычно озадачивает и очаровывает странная способность зеркала мгновенно расшифровывать послания, написанные или напечатанные задом наперед. Взрослых людей этим не удивишь. Они настолько свыклись с этой особенностью зеркал, что воспринимают ее как нечто само собой разумеющееся. Они думают, что ничего непонятного тут нет. Так ли это? Все ли тут вам самим до конца понятно?

Разрешите смутить вас простым вопросом: почему зеркало переставляет только правую и левую стороны всех вещей, а не верх и низ? Подумайте хорошенько. Зеркало имеет абсолютно плоскую и гладкую поверхность. Его левая и правая части ничем не отличаются от верхней и нижней частей. Так почему же оно может переставить вашу левую и правую руки, но не может поменять местами ноги и голову? Каждая строка приведенного выше четырехстишия «перевертыша» (Jabberwocky) читается справа налево. Если вы посмотрите на эти строчки в зеркало, они пойдут слева направо, но верхняя строка останется верхней, а нижняя — нижней. Почему? Зеркало переставляет правую и левую стороны. А что будет, если повернуть его по часовой стрелке на четверть оборота? Перевернется ли отражение вашего лица? Всем, конечно, известно, что ничего подобного не случится. Тогда откуда же это настойчивое загадочное предпочтение правому и левому? Почему зеркало может вывернуть комнату по горизонтали, а опрокинуть ее вверх дном не может?

Я надеюсь, что эти вопросы заставят вас хоть на мгновение почувствовать себя в шкуре той любопытной обезьянки, которая созерцает свое отражение в зеркале. Это действительно «хитрые» вопросы. Проверьте их на своих друзьях. Все шансы за то, что они будут озадачены не меньше вашего. Смущенного смеха и сбивчивых попыток объяснения будет хоть отбавляй, но вряд ли кто даст прямой и четкий ответ. По своему обращению с зеркалами взрослые люди больше похожи на кошек и собак, чем на обезьян. Они считают, что отражение в зеркале объяснений не требует, и не пытаются понять до конца, почему именно так «работает» зеркало.

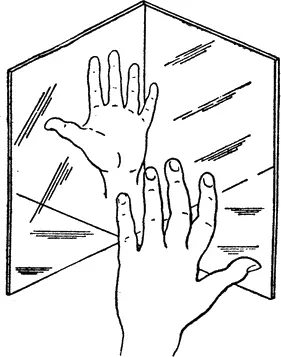
Положение можно запутать еще больше. Совсем легко сделать зеркало, которое вовсе не переставляет правую и левую стороны. Для этого можно взять, например, два прямоугольных зеркала без рамок и поставить их на стол, как показано на рис. 1. Зеркала должны быть взаимно перпендикулярными и касаться друг друга одним краем. Наклонитесь и посмотрите в такое составное зеркало. Если отражение вашего лица уже или шире обычного, отрегулируйте зеркала, пока лицо не станет нормальным. Но будет ли оно таковым? Подмигните правым глазом. При этом ваш двойник вместо того, чтобы подмигнуть левым глазом — то есть глазом, расположенным напротив вашего правого, — подмигнет своим правым глазом. Отражение в таком зеркале отличается от «нормального» зеркального изображения, но оно является истинным, неперевернутым изображением. Вы впервые видите себя в зеркале точно в таком же виде, в каком вас видят другие!

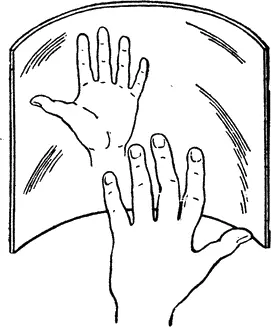
Изготовить зеркало, обладающее описанным свойством, можно и по-другому — слегка изогнув тонкий полированный лист металла (рис. 2). Если вы добьетесь неискаженного изображения, оно будет и неперевернутым. Это легко проверить, моргнув глазом или высунув язык на сторону. Такие изогнутые зеркала были известны уже древним грекам, и Платон описал их в своих диалогах. Про них пишет и древнеримский поэт Лукреций в четвертой книге своей великой научной поэмы «О природе вещей», в главе о зеркалах.

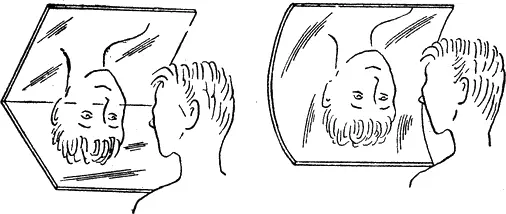
Что случится с вашим отражением, если повернуть одно из таких загадочных зеркал на четверть оборота? Изображение мгновенно перевернется вверх ногами (рис. 3)! Значит, в определенном положении такое зеркало ничего не переставляет в изображении — ни правую сторону с левой, ни верхнюю с нижней. В другом же положении то же самое зеркало меняет местами верх и низ!

Предмет явно заслуживает дальнейшего изучения (так, наверное, говорит себе шимпанзе, размышляя о том, что видит в зеркале). Это изучение мы начнем со следующей главы, где разберемся подробно, что происходит в зеркале с одномерными и двумерными геометрическими фигурами. В процессе изучения придется познакомиться со многими удивительными научными истинами. Некоторые из них будут легковесными, а другие — не такими уж пустячными. Два открытия, принадлежащих к числу выдающихся научных свершений века, тесно связаны с проблемой правого и левого и природой зеркальных отображений. Это ниспровержение закона сохранения четности физиками и открытие биологами спирального строения молекулы, которая несет генетический код. Поэтому в последних главах книги русло нашего исследования приведет читателя к самым глубоким и мало изученным водам океана современной науки.

Мы живем в мире трех измерений, или, как иногда говорят для краткости современные геометры, в 3-пространстве. Каждое твердое тело можно измерить вдоль трех осей: север — юг, восток — запад и верх — низ. (Один приятель рассказывал мне, что у них в колледже преподаватель математики, человек с причудами, объяснял существование этих трех осей следующим образом: сперва он бегом пересекал аудиторию поперек, затем вдоль — по центральному проходу, — а после этого несколько раз подпрыгивал на месте.) Изучением геометрических фигур в 3-пространстве занимается стереометрия. Если мы ограничимся рассмотрением двух измерений, то получим планиметрию, то есть геометрию фигур, начерченных на двумерной поверхности — в 2-пространстве. Можно сделать еще один шаг вниз по этой лестнице и рассмотреть фигуры 1-пространства — одномерные фигуры, которые помещаются на прямой линии. Полезно разобрать природу зеркальных отображений во всех трех перечисленных пространствах.