Мартин Гарднер - Этот правый, левый мир

Упражнение 2.Сколько плоскостей симметрии у куба?

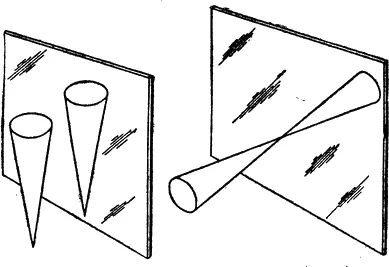
Для совмещения симметричного трехмерного предмета со своим зеркальным изображением может потребоваться поворот в 3-пространстве. Предположим, вы подносите к зеркалу конический стаканчик с мороженым. Если держать его, как показано на рис. 11 слева, чтобы плоскость зеркала была параллельна одной из плоскостей симметрии конуса, то можно совместить предмет с изображением, просто сдвинув их вместе. Но если конус направлен вершиной в сторону зеркала (правая часть рис. 11), то в этом случае, как говорят, предмет и отражение будут иметь разную ориентацию в 3-пространстве. Для того чтобы совместить эти две фигуры, одну из них необходимо повернуть так, чтобы оба конуса были сориентированы одинаково. В данном случае сферу вращать никогда не придется, потому что плоскость зеркала всегда будет параллельна одной из бесчисленного множества плоскостей симметрии сферы.

У асимметричных пространственных объектов нет ни одной плоскости симметрии; их никогда нельзя совместить с отражением в зеркале независимо от ориентации — это, например, всем известные спиральная пружина и винтовая лестница. Точно так же, как спираль является асимметричной фигурой в плоскости, пружина — трехмерная спираль — асимметрична в 3-пространстве. Как ни пытайтесь, вам не удастся плоскостью рассечь пружину на две зеркально симметричные половинки. Поднесите пружину к зеркалу. Как бы вы ее ни поворачивали, в зеркале она всегда «получается не такой».

Каждая асимметричная фигура имеет зеркального двойника, который во всех деталях совпадает с ней — только «получается не такой». Две асимметричные фигуры, являющиеся зеркальным изображением одна другой, называются энантиоморфами. Каждая из них энантиоморфна другой. Знакомый пример пары энантиоморфов — ваши собственные руки. Посмотрите на них, сблизив ладони, и увидите, что одна — зеркальное отражение другой. Этот пример стал таким обыденным, что любые энантиоморфы различают, называя одни из них «правыми», а другие «левыми». Пара перчаток, ботинок или ваши уши — все это энантиоморфы.

Если составная часть какого-нибудь предмета включает винт или пружину, то он асимметричен; и штопор, и винт, и гайка, все что с винтовой резьбой, асимметричны. Винты обычно делают так, что они ввинчиваются при вращении их по часовой стрелке. Про такие винты говорят, что они с правой резьбой. Для специальных целей изготовляются и винты с левой резьбой. В автомобилях, например, шпильки и гайки, которыми крепятся колеса, с одной стороны автомобиля имеют правую резьбу, а с другой — левую. (Это сделано потому, что при вращении колес гайки по обе стороны автомобиля стремятся раскручиваться.) Разная резьба не дает возможности резьбовому соединению разболтаться. Цоколи электрических лампочек, которые вы покупаете в магазине, имеют правую резьбу, но лампочки, которые до недавнего времени можно было видеть в вагонах нью-йоркского метро, имели левую резьбу! Это была мера против тех, кто выкручивал их и брал себе домой. (Теперь вместо ламп накаливания в метро употребляются лампы дневного света, они вставляются в специальные зажимы.) А слыхали ли вы когда-нибудь о левом штопоре? Попробуйте сделать такой и подшутить над кем-нибудь. Дайте его тому, кто хочет открыть бутылку, и посмотрите, скоро ли он сообразит, почему у него ничего не получается! Если же вращать такой штопор против часовой стрелки, он, конечно, ввернется в пробку не хуже всякого другого.

Упражнение 3.Можете ли вы сказать, почему во всем мире в основном используется правая резьба?

Посмотрите вокруг себя, и вы будете удивлены тем, сколь многие предметы, сделанные человеком, в целом симметричны, хотя бы внешне. В некоторых случаях предметы, кажущиеся симметричными на первый взгляд, при ближайшем рассмотрении таковыми не оказываются. Например, ножницы. Их лезвия могут в принципе пересекаться двумя различными способами — один зеркальное отражение другого. Большинство ножниц сделано с расчетом на то, что человек будет пользоваться ими, держа их в правой руке. Если вы не левша, то знаете, как неудобно стричь ногти на правой руке, держа ножницы в левой. Дело не только в том, что вы правша и левой рукой вам работать вообще неудобно: ножницы сделаны для пользования ими правой рукой, а вы держите их левой. Нажимать при этом на ручки так, чтобы ножницы резали как следует, очень неловко. В связи с этим выпускаются специальные ножницы для портных-левшей и вообще всех «леворуких» людей, которым часто приходится работать с ножницами.

Симметричен ли автомобиль? В общих чертах да, но, присмотревшись к деталям, например к расположению рулевого колеса, мы увидим, что это, конечно, не так. Энантиоморфом американских автомобилей являются, например, английские, которые приспособлены для левостороннего движения, поэтому руль у них справа. А симметричен ли самолет, летящий высоко в небе? Днем — да, но не ночью, когда на его левом крыле загорается зеленый огонь, а на правом — красный. Симметричен ли электрический вентилятор? Нет, потому что его лопасти вырезаны из винтовой поверхности. Если заменить их энантиоморфными лопастями, вентилятор будет гнать воздух назад, а не вперед. Винты самолетов и кораблей также асимметричны. Как вы думаете, симметричен кусок веревки? Может быть. Присмотритесь повнимательнее. Если она состоит из крученых ниток, значит, симметрия отсутствует, скрученная нитка — та же спираль, а в зеркальном отражении она будет закручиваться в другую сторону.

Упражнение 4.Какие из перечисленных ниже предметов асимметричны?

1. Хоккейная клюшка.

2. Спиннинг.

3. Машинка для точки карандашей.

4. Вилка.

5. Серп.

6. Саксофон.

7. Разводной гаечный ключ.

Лист Мёбиуса — хорошо известный топологический курьез — асимметричен. Если вы закрутите полоску бумаги на полоборота и склеите концы, то получите поверхность, у которой только одна сторона и только один край. Но это закручивание на полоборота можно сделать двояким способом — вправо или влево. Изогнете в одну сторону — получите лист Мёбиуса одного типа. Изогнете в другую — получите его энантиоморф.

Простой узел, завязанный на замкнутой веревочной петле, тоже может быть правым и левым. На рис. 12 изображена пара таких энантиоморфных узлов. Как бы вы ни старались, вам не удастся превратить узел в его зеркального близнеца. Обращали ли вы когда-нибудь внимание на то, что, скрещивая руки на груди, вы «завязываете себя» именно в такой узел? Следующий наглядный пример поможет вам понять это. Разложите перед собой на столе или дайте кому-нибудь подержать кусок веревки длиной около метра. Скрестите руки, взяв предварительно веревку за концы; теперь разъедините руки. Раньше у вас они были «завязаны узлом», теперь узел перейдет на веревку. В зависимости от того, как вы сложите руки, получится «правый» или «левый» узел. Отложите в сторону завязанный конец веревки и проделайте то же самое с другим концом, но теперь сложите руки «по-другому». Получившийся узел будет зеркальным отражением первого. Если вы проделаете все это перед зеркалом, то увидите, что ваш энантиоморф в зеркале и руки-то складывает «по-другому» и узел у него получается другой — если у вас левый, то у него правый, и наоборот.