Мартин Гарднер - Этот правый, левый мир

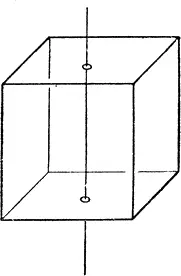
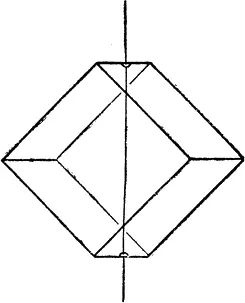
Все три описанные кристаллические решетки симметричны в том смысле, в каком мы до сих пор использовали это слово, то есть они совместимы со своими зеркальными отражениями. Кроме того, эти решетки обладают и многими другими типами симметрии, изучением которых занимаются кристаллографы, например разными видами осевой симметрии. Это означает, что если вращать решетку определенным образом вокруг некоторой оси, то после поворота она примет точно такой же вид, как имела до него. Если, например, ось проходит через куб, как показано на рис. 25, вы можете, поворачивая, перевести его в четыре различных положения, которые по всем своим свойствам абсолютно одинаковы. Такая ось называется осью симметрии четвертого порядка. Легко видеть, что у куба четыре таких оси. Если ось проходит через куб, как показано на рис. 26, то поворотами вокруг такой оси его можно поместить в одно из двух одинаковых положений. Такая ось называется осью симметрии второго порядка. Таких осей у куба шесть.

Кристаллы могут обладать осями симметрии второго, третьего, четвертого и шестого порядков. Симметрию пятого порядка кристаллическая решетка иметь не может. Вы можете выложить паркет из треугольников, квадратов и шестиугольников, но не из пятиугольников. По той же причине пятиугольные («пентагональные»), формы никогда не встречаются у трехмерных кристаллов. В живой природе они встречаются часто. Большинство цветов (например, примула) и некоторые животные (например, морская звезда) обнаруживают пентагональную симметрию, но пентагональных кристаллов нет. Согласно строгим законам геометрии, структура кристаллической решетки не может иметь осей симметрии пятого порядка.

Как мы уже видели, у куба есть оси второго и четвертого порядков. А есть ли у него ось третьего порядка? Большинство людей поражается, когда им говорят, что у куба есть и такие оси — целых четыре штуки.

Упражнение 8.Найдите у куба четыре оси симметрии третьего порядка. Иными словами, найдите четыре такие оси, чтобы, вращая куб вокруг любой из них, можно последовательно добиться только трех (ни больше, ни меньше) абсолютно одинаковых положений.

Все эти примеры осевой симметрии можно назвать выполнимыми операциями по той простой причине, что они могут быть произведены в действительности. Тогда симметрию отражения следует называть невыполнимой операцией, потому что нет способа осуществить ее над каким-нибудь реальным твердым телом. Как мы уже знаем, двумерный плоский объект можно отразить, если взять его и перевернуть, но для этого мы должны оперировать с двумерным объектом в 3-пространстве. Точно так же мы смогли бы выполнить отражение над трехмерным твердым телом, если бы знали способ перевести его в пространство высшей размерности. Поскольку такого способа у нас нет, кристаллографы и называют такую операцию невыполнимой. Есть и другие типы невыполнимых операций симметрии, но мы и так уже уделили им больше внимания, чем следует. Симметрия кристаллов — сложная и увлекательная тема, на которую написано огромное количество книг; мы должны устоять перед искушением и не вдаваться в детали. Эта книга — о симметрии вообще. Мы занимаемся кристаллами лишь потому, что нас интересует симметрия отражения, и хотим знать, есть ли у кристаллов плоскость симметрии, совместимы ли они со своими зеркальными отражениями.

Многие минералы находят в виде бесформенных глыб, внешний вид которых не дает никаких или почти никаких указаний об их кристаллическом строении. Счастливым исключением является алмаз — форма кристаллического углерода. Его обычно находят в виде отдельных кристаллов, иногда поразительно правильной формы. Благодаря решетке кубической формы алмаз имеет несколько кристаллических разновидностей. Наиболее часто встречается форма, показанная на рис. 27 слева и известная в геометрии под названием октаэдр (восьмигранник). Обратите внимание на то, что все грани являются равносторонними треугольниками. Фигуры, ограниченные подобно этой плоскими гранями, называются многогранниками. Если многогранник можно положить на стол любой из его плоских сторон, он называется выпуклым. Если все ребра многогранника имеют одинаковую длину, а углы всех граней — одинаковую величину, он называется правильным многогранником.

Имеется только пять правильных выпуклых многогранников: тетраэдр, гексаэдр (куб), октаэдр, додекаэдр и икосаэдр. Иногда их называют «телами Платона», потому что Платон написал о них много интересного. В природе их находят в довольно необычных местах; недавно обнаружили, что некоторые вирусы имеют форму тетраэдров, додекаэдров и икосаэдров!

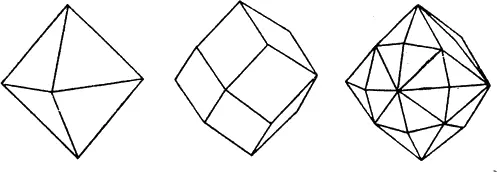
Ромбический додекаэдр (см. рис. 27, в центре) и гексагональный октаэдр (см. рис. 27, справа) —две другие поразительно красивые кристаллические формы, которые иногда имеет алмаз. Все три перечисленные кристаллические формы симметричны; каждая обладает многими плоскостями и осями симметрии, расположение которых определяется свойствами основной кристаллической решетки. Углерод приобретает кристаллическое строение алмаза, если его подвергнуть высокому давлению. Атомы в его решетке упакованы настолько плотно, что сблизить их еще больше почти невозможно; именно поэтому алмаз — самое твердое из веществ, известных в природе. Углерод может иметь кристаллическую решетку и другой формы, где атомы расположены менее тесно, — это графит, используемый в обычных карандашах, а когда кристаллическая структура разрушается полностью, получается древесный уголь или сажа. Вся разница между сажей, покрывающей печные стенки, и бриллиантом, сверкающим на женском пальце, заключается в различном порядке расположения углеродных атомов!

Очень распространенной кристаллической формой, почти такой же, как кубическая, является ромбоэдр, показанный на рис. 28. Все шесть граней у него в точности одинаковы, это ромбы, и все ребра имеют одинаковую длину. Это как будто куб, сжатый с двух противоположных углов. Такую форму имеют часто встречающиеся кристаллы минерала кальцита (углекислый кальций), а также азотнокислого натрия. Достаточно ли ясно вы представляете себе их форму, чтобы решить, симметрична она или нет?