Макс Тегмарк - Наша математическая вселенная

Чтобы объяснить, как устроены атомы, датский физик Нильс Бор предложил в 1913 году весьма радикальную идею. Возможно, не только материя и свет квантуются (то есть существуют в виде дискретных фрагментов, подобных деталям «Лего»). Это может относиться и к свойствам движения . Что если движение не непрерывно, а скачкообразно, как в компьютерной игре «Пэкмен» или в фильмах с Чарли Чаплином, где частота кадров была слишком низкой? На рис. 7.5 показана модель атома Бора: круговые орбиты разрешены, лишь если их окружности имеют определённые, магические длины. Существует наименьшая орбита, помеченная n = 1, а далее есть орбиты большего размера ( n = 2 и т. д.), радиусы которых в n 2раз больше радиуса минимальной орбиты. [33]

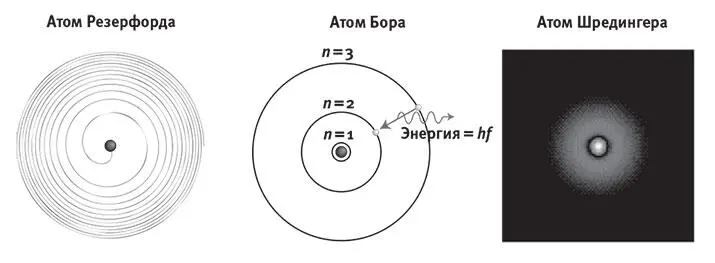
Рис. 7.5.Эволюция наших представлений об атоме водорода. Классическая (планетарная) модель Эрнеста Резерфорда, к сожалению, была неустойчивой: в ней электрон по спирали падал на находящийся в центре протон (я изображаю, как бы это выглядело, если бы электрическое взаимодействие было в 20 раз сильнее; иначе спираль имела бы около 100 тыс. витков, что невозможно нарисовать). Модель Бора удерживает электрон на дискретных орбитах, пронумерованных n = 1, 2, 3, …, между которыми он перепрыгивает, когда испускает или поглощает фотоны. Эта модель не работает для всех атомов, кроме атома водорода. В модели Шрёдингера один электрон находится одновременно во многих местах электронного облака, форма которого задаётся математической функцией Ψ.

Первый, самый очевидный успех состоял в том, что боровский атом не коллапсировал, как классический ( рис. 7.5 , слева). Когда электрон находится на самой внутренней орбите, просто не существует меньшей орбиты, куда он мог бы перескочить. Однако модель Бора объясняла далеко не только это. Высокие орбиты обладают большей энергией, чем низкие, а полная энергия сохраняется. Поэтому, когда электрон, будто «Пэкмен», соскакивает на более низкую орбиту, избыток энергии должен быть испущен атомом в виде фотона ( рис. 7.5 ), а чтобы занять более высокую орбиту, электрон должен быть способен заплатить энергетическую «цену», поглотив фотон с нужной энергией. Поскольку существует только дискретный набор орбитальных энергий, атом может испускать и поглощать фотоны лишь с «магическими» энергиями. Иными словами, атом может испускать и поглощать свет только на определённых частотах. Это разрешает давнюю проблему. В спектре солнечного света ( рис. 2.5 ) обнаружены тёмные линии на определённых частотах (то есть некоторые цвета отсутствуют), а при изучении горячих светящихся газов в лаборатории наблюдалось, что каждый тип атомов имеет уникальный спектральный «отпечаток» в виде частот света, которые он может испускать и поглощать. Боровская модель атома не просто объяснила существование этих спектральных линий, но и позволила точно вычислить их частоты для водорода. [34]

Это был отличный результат, и Бор получил за него Нобелевскую премию (как и большинство остальных учёных, упомянутых в этой главе). Плохой новостью стало то, что боровская модель не работала для атомов, отличных от водорода, за исключением случая, когда с них сорваны все электроны, кроме одного.

Несмотря на первые успехи, физики по-прежнему не знали, что делать с этими странными, на первый взгляд произвольными квантовыми правилами. Что они в действительности означают? Почему угловой момент квантуется? Есть ли этому более глубокое объяснение? Одно из них предложил Луи де Бройль: электроны (а на самом деле все частицы) обладают волновыми свойствами, подобно фотонам. Во флейте стоячие звуковые волны могут колебаться только на некоторых определённых частотах. Может быть, чем-либо аналогичным определяются и частоты, с которыми электроны обращаются в атомах?

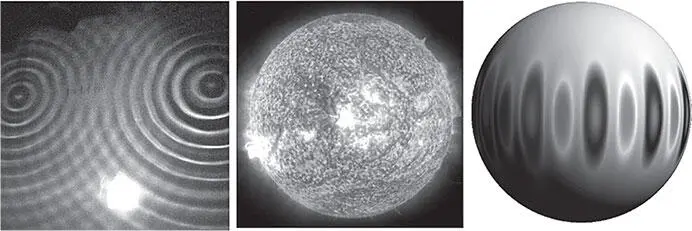
Рис. 7.6.Волны в ёмкости с водой ( слева ) и на Солнце ( справа ).

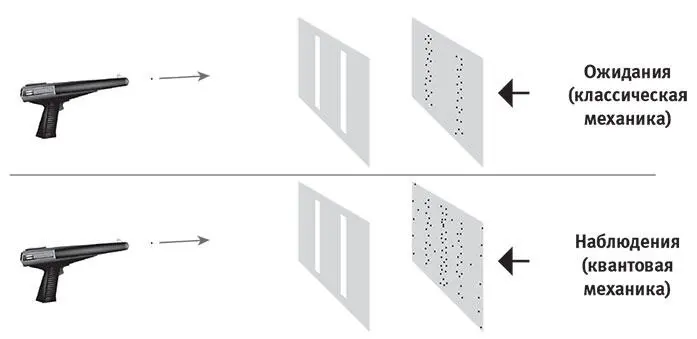
Рис. 7.7.Если стрелять частицами (скажем, электронами или фотонами из лазерного ружья) по барьеру с двумя вертикальными щелями, то, согласно предсказанию классической физики, частицы будут попадать в детектор вдоль двух вертикальные полос позади щелей. Квантовая механика предсказывает, что каждая частица будет вести себя как волна, проходя через обе щели в квантовой суперпозиции, интерферируя при этом сама с собой и образуя интерференционную картину ( рис. 7.6 ). Этот знаменитый эксперимент демонстрирует, что квантовая механика корректна: частицы регистрируются у целого ряда вертикальных полос.

Две волны способны без помех проходить друг сквозь друга, как круги на поверхности воды ( рис. 7.6 , слева). В любой момент их воздействия просто складываются. В некоторых местах видно, что гребни двух волн складываются в ещё более высокий гребень (конструктивная интерференция), в других местах гребень одной волны подавляется впадиной другой, оставляя воду совершенно невозмущённой (деструктивная интерференция). На поверхности Солнца ( рис. 7.6 , справа) наблюдаются звуковые волны в горячем газе (плазме). Если такая волна обойдёт вокруг Солнца (справа), она погасит сама себя в результате деструктивной интерференции, если только не совершит за время обхода целое число колебаний, чтобы, вернувшись, совпасть с самой собой. Это значит, что, как и флейта, Солнце колеблется только на некоторых определённых частотах. [35]

В своей диссертации 1924 года де Бройль применил это рассуждение к волнам, распространяющимся не по Солнцу, а по атому водорода, и получил точно те же частоты и энергии, которые предсказывала модель Бора. А двухщелевой эксперимент ( рис. 7.7 ) более явно продемонстрировал, что частицы ведут себя как волны.

Волновая картина делает нагляднее и объяснение того, почему атомы не коллапсируют, как предсказывает классическая физика: если попытаться заключить волну в очень малое пространство, она немедленно начнёт распространяться в стороны. Например, если дождевая капля падает на поверхность воды в тазу, она сначала возмущает воду лишь в очень небольшой области, с которой она соприкоснулась, но возмущение начинает быстро распространяться во все стороны в виде кольцевых волн ( рис. 7.6 ). В этом суть принципа неопределённости Гейзенберга . Вернер Гейзенберг показал: если зажать некий объект в малую область пространства, он приобретёт огромный случайный импульс, который заставит его двигаться и чувствовать себя менее стеснённым. Иными словами, объект не может одновременно иметь точное положение и точную скорость! [36]Это означает, что если атом водорода попробует коллапсировать ( рис. 7.5, слева), притянув электрон к протону, то растущая «зажатость» придаст электрону достаточный импульс, а с ним и скорость, чтобы вновь улететь на высокую орбиту.