Макс Тегмарк - Наша математическая вселенная

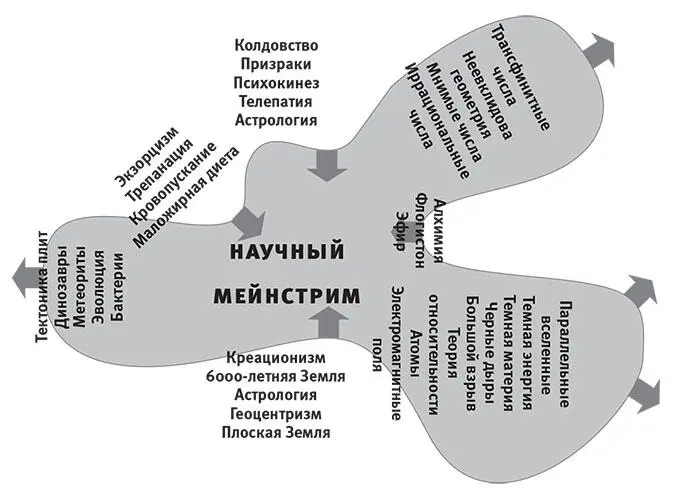
Рис. 10.1.Граница того, что считается мейнстримом, постоянно меняется.

Так какая же из моих статей вызвала столь острую реакцию: остановитесь — или сломаете карьеру? Чему столь далёкому от нынешней границы мейнстрима ( рис. 10.1 ) была она посвящена, что этот профессор почувствовал необходимость вернуть меня в лоно науки? Она была о том, что наш физический мир — это гигантский математический объект. И в этой главе мы начнём его изучать.

Каков же ответ на главный вопрос жизни, Вселенной и всего такого? В книге «Автостопом по Галактике» Дугласа Адамса выясняется, что ответ на этот вопрос — 42, однако самой сложной частью задачи оказалось отыскание самого вопроса. В действительности, хотя наши любознательные предки задавались глобальными вопросами, их поиски «теории всего» менялись вместе с ростом знаний. По мере того как древние греки заменяли мифологические объяснения механическими моделями Солнечной системы, их акценты в этих вопросах смещались с почему на как .

С тех пор сфера наших вопросов сократилась в одних областях и разрослась в других ( рис. 10.1 ). Некоторые вопросы отброшены как наивные или ошибочные, вроде объяснения размеров планетных орбит исходя из первичных принципов (это было популярно в эпоху Возрождения). То же самое может случиться с модными нынче попытками предсказания количества тёмной энергии в космосе, если окажется, что её плотность в наших окрестностях является исторической случайностью ( гл. 6 ). Тем не менее наша способность отвечать на другие вопросы превзошла самые смелые ожидания прежних поколений. Ньютон был бы поражён, узнав, что мы сумели определить возраст Вселенной с точностью до 1 % и узнали устройство микромира в достаточной мере, чтобы сконструировать «Айфон».

Я считаю шутку Дугласа Адамса про 42 очень удачной, поскольку математика играет исключительную роль во всех этих успехах. [63]Та идея, что Вселенная в некотором смысле является математической, восходит по меньшей мере к пифагорейцам и породила многовековую дискуссию физиков и философов. Галилей утверждал, что Вселенная — это «величественная книга», написанная на языке математики. Лауреат Нобелевской премии по физике Юджин Вигнер в 60-х годах XX века настаивал, что «невероятная эффективность математики в естественных науках» нуждается в объяснении.

Фигуры, паттерны и уравнения

Мы переходим к рассмотрению по-настоящему радикального объяснения. Однако прежде необходимо уточнить, что именно мы пытаемся объяснить. Пожалуйста, оторвитесь на несколько секунд от чтения и оглядитесь. Где вся эта математика, которой мы собираемся заниматься? Разве математика — это не наука о числах? Вероятно, вам на глаза попадётся несколько чисел, например пагинация в этой книге, но это лишь символы, изобретённые и изображённые людьми, так что вряд ли они отражают математическую сущность Вселенной в каком-либо глубоком смысле.

Из-за нашей системы образования многие приравнивают математику к арифметике. Но математика, как и физика, пришла к постановке более глубоких вопросов. Например, в приведённой выше цитате Галилей говорит о геометрических фигурах вроде окружностей и треугольников как о математических. Видите ли вы вокруг себя геометрические узоры или фигуры? (Дизайн вроде прямоугольной формы книги не в счёт.) Но попробуйте бросить камешек и посмотрите, какую красивую форму придаёт природа его траектории! Галилей сделал замечательное открытие ( рис. 10.2 ): траектория любых предметов имеет одинаковую форму, называемую перевёрнутой параболой . Более того, форму этой параболы можно описать простым уравнением: x = y 2, где x — горизонтальное положение, y — вертикальное положение (высота). В зависимости от начальной скорости и направления эта форма может растягиваться и по вертикали, и по горизонтали, однако она всегда остаётся параболой.

Когда мы наблюдаем, как объекты движутся по орбитам в космосе, мы открываем другую повторяющуюся форму, показанную на рис. 10.3 — эллипс . Уравнение x 2+ y 2= 1 описывает точки, лежащие на окружности, а эллипс — это просто растянутая окружность. В зависимости от начальной скорости, направления движущегося по орбите объекта и массы, вокруг которой он движется, форма этой орбиты может оказываться растянутой или наклонённой, однако всегда остаётся эллипсом. Более того, оконечность сильно вытянутого эллипса почти точно совпадает с параболой, так что все эти траектории — просто части эллипсов. [64]

Рис. 10.2.Когда вы что-нибудь подбрасываете, траектория полёта предмета всегда имеет форму перевёрнутой параболы, если только он с чем-нибудь не столкнётся в полёте и если можно пренебречь сопротивлением воздуха.

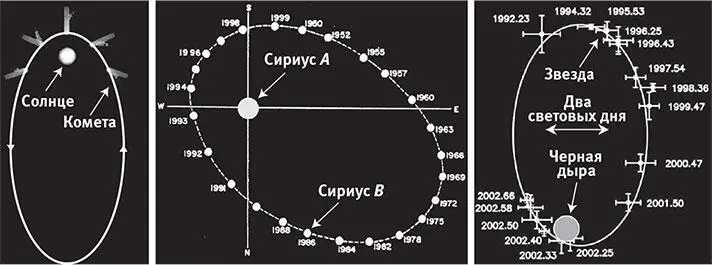
Рис. 10.3.Когда один объект обращается по орбите вокруг другого под действием гравитации, его орбита всегда имеет одну форму, эллипс, который представляет собой просто окружность, растянутую в одном направлении (так будет, если нет источников трения и если мы игнорируем эйнштейновские поправки к ньютоновской теории гравитации, которые обычно ничтожны, если мы не рядом с чёрной дырой). Орбита остаётся эллипсом для самых разных объектов: и для кометы, обращающейся вокруг Солнца ( слева ), и для белого карлика — мёртвой звезды, обращающейся вокруг Сириуса A , ярчайшей звезды нашего неба, и для звезды, обращающийся вокруг гигантской чёрной дыры в центре Галактики ( справа ), которая в миллион раз массивнее Солнца. (Рисунок справа воспроизводится с разрешения Рейнхарда Гензеля и Райнера Шедела.)

Рис. 10.4.Подобно тому, как изобразительное искусство и поэзия могут выразить многое с помощью немногих символов, так и физика способна сделать это с помощью уравнений. Слева направо и сверху вниз на этих шедеврах описаны: электромагнетизм, околосветовое движение, гравитация, квантовая механика и расширение Вселенной. Мы ещё не нашли уравнений единой «теории всего».

Постепенно люди открыли в природе множество других повторяющихся форм и паттернов, охватывающих не только движение и гравитацию, но и такие разные области, как электричество, магнетизм, свет, теплота, химия, радиоактивность и субатомные частицы. Эти паттерны складываются в законы физики . Как и форму эллипса, эти законы можно описать, применяя математические уравнения ( рис. 10.4 ). Почему?