Макс Тегмарк - Наша математическая вселенная

Числа

Уравнения — не единственный скрытый в природе намёк на математику: есть также числа . Я говорю не о творениях рук человеческих, вроде пагинации в этой книге, а о числах, которые выражают фундаментальные свойства нашей физической реальности. Сколько карандашей вы сможете расположить так, чтобы все они были перпендикулярны (под углом 90°) друг другу? Три: их можно разместить, например, вдоль трёх стыков стен и пола в углу вашей комнаты. Откуда взялось число 3? Мы называем его размерностью пространства, но почему существует именно 3 измерения, а не 2, 4 или 42? Почему в нашей Вселенной существует (насколько мы можем судить) ровно шесть типов кварков? Есть много других «встроенных» в природу целых чисел ( гл. 7 ), которые описывают, какого типа элементарные частицы существуют.

И, вдобавок к математическим гостинцам, существуют закодированные в природе величины, которые не являются целыми числами и требуют для записи дробных значений. Согласно моим подсчётам, природа закодировала 32 таких фундаментальных числа. Относится ли к ним число, которое появляется на индикаторе весов, когда вы встаёте на них после ванны? Нет, оно не в счёт, поскольку является мерой чего-либо (вашей массы), что день ото дня изменяется, а значит, не является фундаментальным свойством нашей Вселенной. Что можно сказать о массе протона (1,672 622 × 10 –27кг) или о массе электрона (9,109 382 × 10 –31кг), которые кажутся неизменными во времени? Они также не в счёт, поскольку измеряются в килограммах, а это произвольная единица массы, придуманная людьми. Но если вы разделите одно из этих двух чисел на другое, получится нечто поистине фундаментальное: протон примерно в 1836,15 267 раз массивнее электрона. [65]Значение 1836,15 267 — безразмерное число , подобное π или √2, в том смысле, что его значение не зависит ни от каких человеческих единиц измерения, вроде граммов, метров, секунд или вольт. Почему это значение так близко к 1836? Почему не 2013? Или не 42? Простой ответ состоит в том, что мы этого не знаем. Но, думаю, в принципе мы можем вывести и это число, и все остальные когда-либо измеренные фундаментальные постоянные природы, всего из 32 чисел, перечисленных в табл. 10.1.

Табл. 10.1.Каждое фундаментальное свойство природы, когда-либо подвергнутое измерению, можно вычислить на основе 32 чисел — по крайней мере в принципе. Некоторые из них измерены с очень высокой точностью, тогда как другие экспериментально ещё не определены. Точный смысл этих чисел не имеет значения для нашего изложения, но если вы заинтересовались, то найдёте объяснения в моей статье ( http://arxiv.org/abs/astro-ph/0 511 774 ). Вот только чем определяются значения этих чисел?

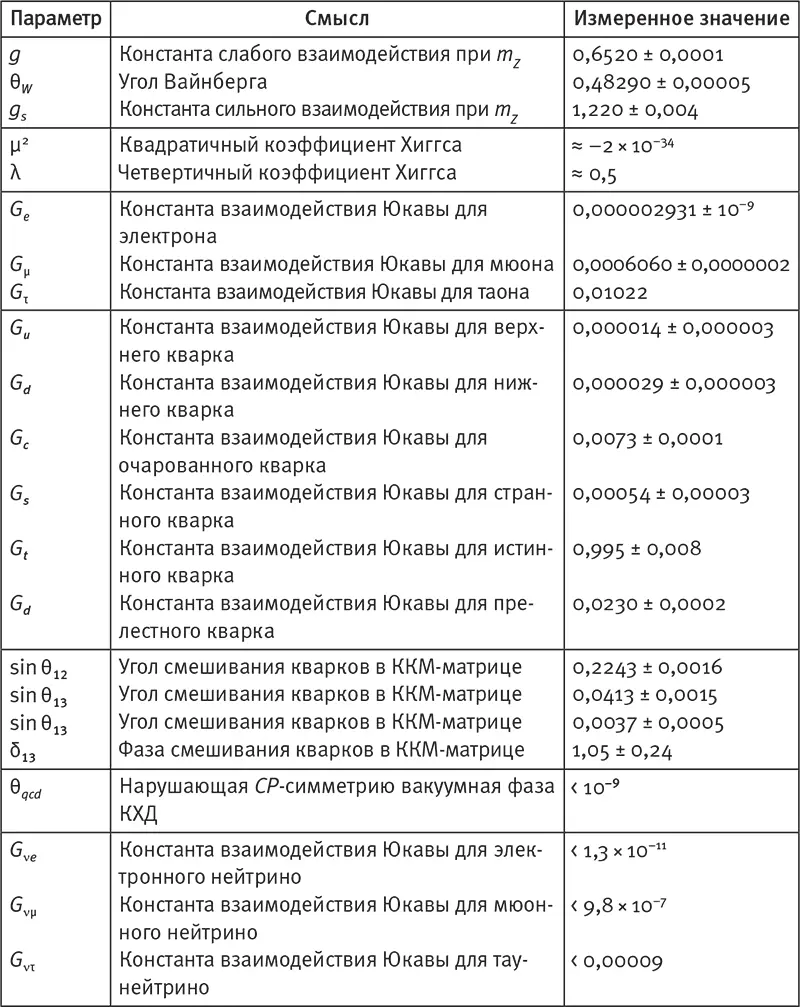
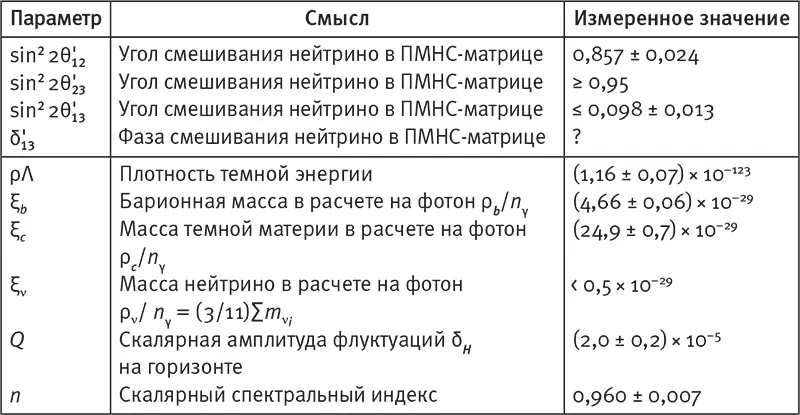
Не пугайтесь названий в таблице: они не имеют отношения к тому, чем мы здесь занимаемся. Суть в том, что в нашей Вселенной есть нечто сугубо математическое, и чем пристальнее мы всматриваемся, тем, похоже, больше математики видим. Что касается природных констант, то имеются сотни тысяч безразмерных чисел, измеренных в разных областях физики: от отношения масс элементарных частиц до отношений характерных длин волн света, испускаемого различными молекулами. С помощью компьютеров, достаточно мощных, чтобы решать уравнения, описывающие законы природы, все до одного эти числа, по-видимому, могут быть определены на основе приведённых в табл. 10.1. Некоторые вычисления и измерения крайне сложны, и их до сих пор не удалось выполнить, а когда удастся, то, возможно, числа в теории и эксперименте не совпадут. Такого рода расхождения не раз случались в прошлом и, как правило, разрешались одним из трёх способов:

1. Кто-нибудь находил ошибку в эксперименте.

2. Кто-нибудь находил ошибку в вычислениях.

3. Кто-нибудь находил ошибку в наших законах физики.

В последнем случае обычно удавалось найти более фундаментальные законы физики — как тогда, когда замена ньютоновских уравнений для гравитации эйнштейновскими позволила объяснить, почему Меркурий обращается вокруг Солнца не по идеальному эллипсу. Во всех случаях ощущение, что в природе есть нечто математическое, лишь усиливалось.

Если вы откроете ещё более точные законы физики, то это может либо сделать число параметров менее 32 ( табл. 10.1 ), позволив вычислить некоторые из этих величин по другим, содержащимся в таблице, — либо увеличить их число за счёт добавления новых величин (относящихся, скажем, к массам новых типов частиц, которые, возможно, будут открыты на Большом адронном коллайдере).

Что делать со всеми этими намёками на присутствие математики в нашем физическом мире? Большинство физиков привыкло, что природа по некоей причине описывается математикой, по крайней мере приближённо, и признают это как факт. В книге «Является ли Бог математиком?» астрофизик Марио Ливио заключает, что «учёные выбрали, над какими проблемами им работать, с учётом того, чтобы эти проблемы можно было решать математическими методами». Но я убеждён, что причина глубже.

Во-первых, почему математика так успешно описывает природу? Я согласен с Вигнером: это требует объяснения. Во-вторых, на страницах этой книги мы постоянно сталкиваемся с уликами, указывающими на то, что математика не просто описывает природу. В некоторых отношениях природа является математической:

1. В гл. 2–4 мы видели, что сама ткань нашего физического мира, его пространство, является чисто математическим объектом в том смысле, что все неотъемлемые свойства пространства — число измерений, кривизна и топология — являются математическими.

2. В гл. 7 мы видели, что «начинка» нашего физического мира состоит из элементарных частиц, которые, в свою очередь, являются чисто математическими объектами в том смысле, что все их неотъемлемые свойства (приведённые в табл. 7.1 числа, например заряд, спин, лептонное число) являются математическими.

3. В гл. 8 мы видели, что существует нечто, возможно, даже более фундаментальное, чем наше трёхмерное пространство с частицами в нём — это волновая функция и бесконечномерное гильбертово пространство, в котором она обитает. Частицы могут создаваться и уничтожаться, а также находиться в нескольких местах одновременно, однако была и всегда будет лишь одна волновая функция, движущаяся по гильбертову пространству в соответствии с уравнением Шрёдингера. И волновая функция, и гильбертово пространство являются чисто математическими объектами.