Макс Тегмарк - Наша математическая вселенная

В контексте ГМВ мы показали, что восприятие течения времени, а также выдвижение предположений и осуществление наблюдений имеют место в каждое единичное наблюдательное мгновение, которое мы переживаем. Это означает, что мы должны выйти за пределы попперовского двухвременного подхода к науке и предложить одновременной подход, применимый к единственному наблюдательному мгновению. Мне нравится мечтать о замечательном карманном пульте управления реальностью. Участвуя в скучных совещаниях, я могу нажать кнопку ускоренной перемотки вперёд. Когда я испытываю восторг, то могу «отмотать» время назад и пережить всё столько раз, сколько захочу. А чтобы превзойти Поппера, я просто нажимаю кнопку «Пауза». Теперь я поистине могу в духе Горация поймать мгновение, рассмотреть его в целостности, прочувствовать и отрефлексировать. В частности, я могу раздумывать над тем, что я предполагаю и что наблюдаю. Если мой мозг работает хорошо, я обнаружу, что моя внутренняя модель реальности отлично согласуется с последними новостями, которые мои чувства поставляют из внешнего мира. И если мой алгоритм научных рассуждений хорош, я обнаружу, что предсказания, которые, как я помню, делаются для этого мгновения, находятся в полном согласии с тем, что действительно происходит. Пока чувства интенсивно трудятся над регистрацией новой информации, которой предстоит быть сознательно воспринятой в будущие наблюдательные мгновения, сознательная часть моей психики занята применением алгоритма научных рассуждений для обновления набора допущений, касающихся более тонких и абстрактных аспектов реальности.

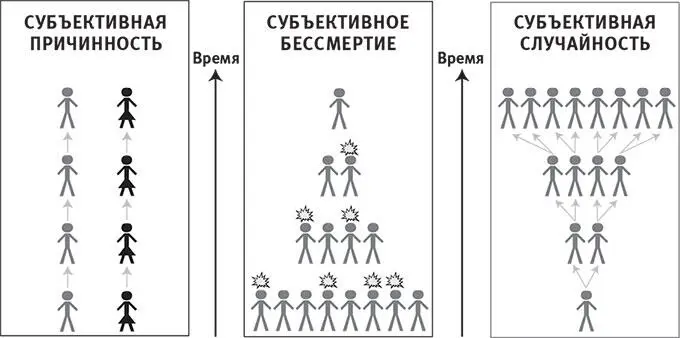
Рис. 11.8.Когда каждое наблюдательное мгновение можно однозначно связать с предшествующим и последующим, мы субъективно воспринимаем это как причинность ( слева ). Когда некоторые последователи исчезают, мы можем воспринимать это субъективно как бессмертие. Когда некоторые субъективно различимые последователи имеют одного и того же предшественника, мы субъективно воспринимаем это как случайность.

Почему вы не муравей?

Так как вы должны рассуждать в своё наблюдательное мгновение, нажав кнопку «Пауза»? Вам понадобится хорошая концептуальная схема, которая позволит не только уложить в неё мультиверс, но и справиться с аргументом Судного дня и иными философскими головоломками. Если вы признаёте гипотезу математической Вселенной, то должны попытаться представить, в какой математической структуре вы живёте. Если эта структура содержит множество наблюдательных мгновений, субъективно ощущаемых как ваши, то вы можете быть любым из них. Если в математике нет чего-либо, нарушающего симметрию и отдающего предпочтение одним мгновениям перед другими, вы с равной вероятностью выберете любое из них. Тем не менее, как я показал в статье о математической Вселенной в 1996 году, вы придёте к заключению:

Следует рассуждать, как если бы ваше наблюдательное мгновение было случайно выбрано из всех возможных.

Два последних десятилетия философы спорят о различных альтернативных способах рассуждения. Эта дискуссия спровоцирована отчасти аргументом Судного дня (который я кратко разберу) и связанными с ним головоломками. Основная идея — нам следует ожидать обнаружить своё сознание не в произвольном месте (как следует из принципа Коперника), а у случайного наблюдателя , имеющего долгую историю. Брэндон Картер сформулировал это как слабый антропный принцип ( гл. 6 ), а Александр Виленкин — как принцип заурядности . Его исследовали Ник Бострём, Пол Олмонд, Милан Чиркович и другие современные философы. В 2002 году Бострём ввёл понятие, ставшее уже общепринятым — сильное допущение о самовыборке (СДСВ):

Каждое наблюдательное мгновение должно анализироваться так, как если бы оно было случайным образом выбрано из всех наблюдательных мгновений референтного класса.

Тонкость в том, как интерпретировать понятие референтный класс , и философы, признающие СДСВ, об этом спорят. Если использовать вариант с наиболее жёсткими опциями и ограничить референтный класс наблюдательными мгновениями ваших копий, которые субъективно неотличимы от ваших собственных наблюдательных мгновений, то мы вернёмся к моему старому подходу. Однако можно прийти к интересным выводам, используя гораздо более либеральный подход. Вы по-прежнему будете приходить к верным заключениям, даже если позволены различные наблюдательные мгновения, лишь бы способ, каким они субъективно ощущаются как различные, не влиял на ответ, который вы ищете. Рассмотрим пример СДСВ — задачу Бострёма о Спящей Красавице.

Претендентки на роль Спящей Красавицы соглашаются участвовать в следующем эксперименте, обо всех условиях которого им сообщают. В воскресенье участница опыта ложится спать. Затем подбрасывается монета с равными шансами упасть на одну из сторон. Если выпадает решка, Красавицу будят и задают ей вопрос только в понедельник. Если выпадает орёл, Красавицу будят и задают вопрос в понедельник и вторник, но когда она вновь ложится спать в понедельник, ей дают препарат, вызывающий амнезию, и это гарантирует, что она не сможет вспомнить предыдущее пробуждение. Всякий раз, когда Красавицу будят, её спрашивают: «Как бы вы оценили шансы, что выпала решка?»

После большого числа публикаций на эту тему философское сообщество разделилось на считающих, что она должна назвать 1/2, и тех, кто придерживается вероятности 1/3. В рамках ГМВ не существует истинной случайности, поэтому заменим монету квантовым измерением, которое в равной мере реализует оба исхода в параллельных двух вселенных III уровня. Теперь в математической структуре, которая соответствует Красавице в момент интервью, есть три субъективно неразличимых наблюдательных мгновения, и все они одинаково реальны:

1. Выпала решка, и это понедельник.

2. Выпал орёл, и это понедельник.

3. Выпал орёл, и это вторник.

Поскольку лишь один из трёх вариантов соответствует выпадению решки, Красавица должна приписать этому событию вероятность 1/3 и испытывать соответствующее субъективное чувство случайности, когда это обнаружит.

Теперь предположим, что экспериментаторы тайно решили перекрасить ей ногти в цвет, зависящий от исхода квантового измерения. Это означает, что не все наблюдательные мгновения являются неразличимыми, но, поскольку красавица не знает, как построен цветовой код, её оценка шансов не должна измениться. Иными словами, мы можем свободно расширять референтный класс, если только это не влияет на результаты.