Виталий Сигорский - Математический аппарат инженера

- 79 -

одного из событий А или В, дважды учитывает m ABисходов, благоприятствующих одновременному появлению А и В. Поэтому из общего числа исходов n появлению событий А или В (или обоих вместе) будут благоприятствовать m A+ m B- m ABисходов, на основании чего имеем

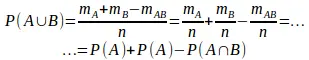
Эта формула получена из каких-либо ограничений относительно характера событий А и В:

для зависимых событий

P(A ∪ B) = P(A) + P(B) -P(A)P A(B),

для независимых событий

P(A ∪ B) = P(A) + P(B) -P(A)(B).

10. Независимость и несовместность. При использовании приведенных соотношений необходимо четко понимать смысл таких свойств событий, как независимость и несовместностью. Условиями независимости событий можно рассматривать каждое из соотношений

P(A ∩ B) = P(A) + P(B); P A(B) = P(B)

Так, при бросании двух игральных костей вероятности событий А(дубль) и В(меньше 6 очков) равны соответственно P(A) = 6/36 = 1/6 и P(B) = 10/36 = 5/18. Одновременному появлению этих событий соответствует подмножество A ∩ B = {(1,1),(2,2)} и его вероятность P(A ∩ B) = 2/36=1/18. Так как P(A ∩ B) B≠ P(A)P(B), то рассматриваемые события являются зависимыми. С другой стороны, событие В при условии наступления события А определяется как подмножество {(1,1),(2,2)} основного множества {(1,1),(2,2), (3,3),(4,4}{(5,5),(6,6)}, и P A(B) = 2/6 = 1/3, т.е. не совпадает с P(B)= 5/18. По соответствующим формулам имеем:

P(A ∩ B) = P(A)P A(B) = 1/6 · 1/3 = 1/18;

P(A ∪ B) = P(A) + P(B) — P(A)P A(B) = 1/6 + 5/18 -1/6 · 1/3 = 7/18.

Очевидно, те же результаты получим, если пример В в качестве дополнительного условия для А. Так как множество {(1,1),(1,2),

- 80 -

(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)}, соответствующее событию В, служит основным для события А, то

P B(A) = 2/10 = 1/5,

и следовательно получаем:

P(A ∩ B) = P(B)P B(A)= 5/18 · 1/5 = 1/18;

P(A ∪ B) = P*A) + P(B) — P(B)P B(A) = 1/6+5/18-5/18· 1/5=7/18.

Общее условие несовместности событий выражается как

P(A ∩ B) = 0,

что соответствует A ∩ B = ∅. Так, в рассматриваемом примере A ∩ B = {(1,1),(2,2)} ≠ ∅, следовательно, события А и В совместны.

Независимые события А и В при ненулевых вероятностях P(A) и P(B) всегда совместны. Действительно, из соотношения P(A ∩ B) = P(A)(B) имеем P(A ∩ B) ≠ 0, а значит и A ∩ B ≠ ∅, что свидетельствует о совместности независимых событий. Однако совместность событий не обязательно влечет их независимость. Из условия A ∩ B ≠ ∅ при P(A ∩ B) ≠ 0 следует лишь, что P(A ∩ B) ≠ 0 и условная вероятность P A(B) ≠ 0. Но может иметь место неравенство P A(B) = P(B), что означает зависимость рассматриваемых совместных событий.

Зависимые события А и В при ненулевых вероятностей P(A) и P(B) могут быть как совместными, так и несовместными. В первом случае A ∩ B ≠ ∅, и поэтому условные вероятности P A(B) и P B(A) не равна нулю, т.е. одно из событий может наступить при условии, что произошло другое событие. Во втором случае A ∩ B = ∅, следовательно, условные вероятности зависимых и несовместных событий P A(B) = P B(A) = 0. Это значит, что пир наступлении события А событие В произойти уже не может, а наступлении события В не может произойти событие А. В то же время из несовместности событий (A ∩ B = ∅) следует их зависимость, что выражается равенством нулю условных вероятностей P A(B) и P B(A). Иначе говоря, если события А и В несовместны, то при наступлении одного из них другое произойти не может, т.е. несовместные событие не могут быть независимыми.

Несовместность совокупности событий A 1, A 2, ..., A n, следует из их попарной несовместимости, т.е. из условия

A i∩ A j= ∅ (i,j = 1,2,..., n; i ≠ j).

- 81 -

Однако полная независимость совокупности событий, вообще говоря, еще не определяется их попарной независимостью. Кроме условий

P(A i∩ A j) = P(A i)P(A j) (i,j = 1,2,..., n; i ≠ j),

должны выполняться также аналогичные условия для любых сочетаний по 3, 4, ... , n событий. Например, для трех событий условие полной независимости выражается системой соотношений:

P(A 1∩ A 2) = P(A 1)P(A 2);

P(A 1∩ A 3) = P(A 1)P(A 3);

P(A 2∩ A 3) = P(A 2)P(A 3);

P(A 1∩ A 2∩ A 3) = P(A 1)P(A 2)P(A 3).

Невыполнение хотя бы одного из этих соотношений свидетельствовало бы о том, что события A 1, A 2и A 3в совокупности зависимы. На практике, однако, попарная независимость обычно влечет за собой и независимость в совокупности.

1. Какова вероятность угадать все шесть номеров (из 49) в спортлото?

2. Из урны, содержащей 8 белых и 12 черных шаров, вынимают один шар. Какова вероятность того, что он будет белым; что он будет черны?

3. Найдите на основе рассмотрения множества событий при бросании двух игральных костей (каждая кость имеет шесть равноправных граней, пронумерованных от 1 до 6) вероятность следующих событий:

а) на одной кости четыре очка, а на другой — меньше четырех;

б) на одной кости число очков вдвое больше, чем на другой;

в) сумма очков меньше пяти;

г) сумма очков больше восьми.

4. Какова вероятность открыть замок автоматической камеры хранения при случайном наборе цифр (замок открывается только при определенных значениях четырех десятичных цифр)?

5. Оцените вероятность того, что в группе из 23 студентов, по крайней мере, у двух студентов дни рождения совпадают.

6. Партия из 10 телевизоров принимается в магазине при условии, что случайно выбранные два из них окажутся исправными. Какова вероятность того, что магазин примет партию, содержащую 4 неисправных телевизора?

7. Два стрелка проводят по одному выстрелу, причем вероятности попадания в цель для них равны соответственно 0,8 и 0,9. Найдите вероятность поражения цели обоими стрелками и вероятность поражения цели хотя бы одни из них.

8. Исследуйте на независимость события А и В при следующих испытаниях:

а) из колоды в 52 карты выбирают одну: А - «туз»; В - «бубна»;

б) бросают две игральные кости: А - «одно очко на первой кости»; В - «четное число очков на второй кости»;

в) бросают три монеты: А - «выпало два герба»; В - «выпало три герба».

- 82 -

9. Исследуйте на несовместность события А и В при бросании игральной кости, если:

а) А - «четыре очка»; В - «четное число очков»;

б) А - «четное число очков»; В - «нечетное число очков».

10. Пять карточек, помеченные цифрами от 1 до 5, тщательно перетасовывают. Какова вероятность того, что:

а) трехзначное число, определяемое номерами трех извлеченных наугад карточек, окажется четным;

б) при случайной раскладке всех карт пять мест с номерами от 1 до 5 ни одна карточка не займет места, отмеченного ее номером;

в) при поочередном выборе всех карточек их номера будут появляться в возрастающим порядке.

11. Из 30 выстрелов по цели отмечено 25 попаданий. Найти относительную частоту попаданий в цель.

Данный текст я (w_cat) набираю руками, опечатки LibreOffice Writer, как положено, выделяет красной волнистой, но если «опечатанное» слово совпадает с существующим в словаре (базе) то опечатку я не замечу и не исправлю, вычислите вероятность такой ошибки :).