Рафаель Роузен - Математика для гиков
- Название:Математика для гиков
- Автор:
- Жанр:
- Издательство:Литагент АСТ
- Год:2016
- Город:Москва
- ISBN:978-5-17-096852-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Рафаель Роузен - Математика для гиков краткое содержание
После прочтения вы сможете использовать в разговоре такие термины как классификация Дьюи, Числа Фибоначчи, равновесие Нэша, парадокс Монти Холла, теория хаоса, подготовитесь к тексту Тьюринга, узнаете, как фильм получает Оскар, и что это за эффект бразильского ореха.
Математика для гиков - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Не все наборы танграм состоят из треугольников и прямоугольников. Один вид – яйцо Колумба – сначала предстает двухмерной фигурой. Потом его делят на детали, у некоторых из них изогнутые края.
1.31. Бархатные канаты как математическая категория
Математическое понятие: цепная линия
Если вы поедете в Сент-Луис в Миссури, вы не сможете не увидеть «Ворота Запада», это громадная постройка из стали и бетона, которая достигает в высоту 630 футов. Достроенная в 1965 году арка символизирует историческую роль Сент-Луиса в качестве ворот на запад для тех, кто колонизировал Северную Америку. Арку можно также рассматривать как дань уважения математике, так как ее форма напоминает цепную линию, своего рода арку, которая образовывается, когда цепь прикрепляют к двум стойкам с обеих сторон, и при этом она ниспадает к земле. (Если быть более точным, то «Ворота Запада» – это перевернутая версия почти цепной линии.) Цепные линии вы можете увидеть в линиях электропередачи между вышками и в форме тяжелого троса, который держит корабль в порту. Вы также можете их увидеть в виде бархатных канатов, которые ограждают людей, стоящих в очереди в кино или на концерт.
Цепные линии похожи на параболы – другой вид кривых, – но уравнение для них было получено лишь в 1691 году тремя математическими титанами: Христианом Гюйгенсом, Якобом Бернулли и Готфридом Лейбницем.
Перевернутые цепные линии часто встречаются в архитектуре, придавая красоту и грацию разным пространствам. Их можно увидеть, например, под террасой «Дома Мила» Антони Гауди, а еще они поддерживают крышу Зимнего сада Шеффилда в Южном Йоркшире в Великобритании.
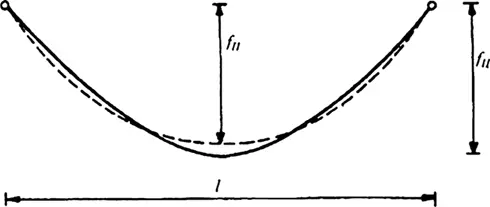
1.32. Как подвесные мосты выдерживают машины?
Математические понятия: фигуры, физика
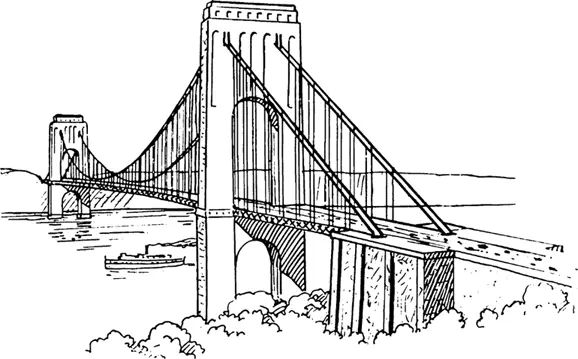
Представьте прекрасное архитектурное сооружение, и вы, вероятно, подумаете о цепном мосте. Эти парящие конструкции узнаваемы благодаря кабелям, которые не только выглядят красиво, но и выполняют важную задачу: они поддерживают проезжую часть, которая проходит под ними. Эти волнообразные кривые также являются примерами парабол, форм, знакомых математикам и которые можно найти во многих местах физического мира.
Если вы помните декартову систему координат из уроков геометрии, то вы также помните, что можете построить параболу с помощью уравнения y=х² . Или вы можете помнить, что парабола относится к классу фигур, известный как коническое сечение, которое образуется, когда плоскость, как лист бумаги, пересекает круговой конус разными способами. (На уроках физики вы, возможно, учили, что кабели передают силу тяжести, оказываемую тяжелой дорогой и машинами на башни моста, которые направляют эту силу вниз в землю.) Кабели также имеют форму парабол отчасти из-за дороги и движения по ней. Без этого веса кабели могли бы принять форму больше похожую на цепные линии, то есть форму, которую принимают такие висячие объекты, как веревки, когда единственной силой, которая на них действует, является гравитация (см. главу 1.31).
Естественно, не во всех мостах есть кабели. Некоторые мосты содержат такие структурные компоненты, как фермы. Они обычно сооружаются из множества компонентов, обычно треугольников, которые соединены так, что вся конструкция ведет себя как единое целое.
2. Часть 2. Поведение
2.1. Почему автобусы подъезжают группами?
Математическое понятие: теория хаоса
Если вы живете там, где ходят автобусы, вы, наверное, замечали, что иногда стоите на остановке намного дольше, чем рассчитывали, а автобусов все нет и нет. Вы смотрите на горизонт, ваша нога нервно стучит по асфальту, и вдруг видите два подъезжающих автобуса. «Черт! – вскрикиваете вы. – Почему они не могут приезжать равномерно? Что не так с транспортной системой в этом идиотском городе?»
Но оказывается, автобусы группируются не потому, что проблема в транспортной системе. На самом деле, это просто неизбежно. Представьте два автобуса, которые выезжают из автобусного парка рано утром в начале смены. Допустим, они выезжают оттуда с десятиминутным интервалом. Если бы автобусу нужно было подъехать к остановке, подождать определенное количество времени и уехать, то они бы не группировались. Но, естественно, на каждой остановке он должен набрать пассажиров, а время, которое нужно человеку, чтобы сесть в автобус, у всех разное. (Сравните пожилого человека с тростью и 10-летнего мальчика.) Более того, на некоторых остановках собирается огромное количество ожидающих пассажиров. (Возможно, эта остановка находится рядом со школой и каждый день примерно в 3 часа дня толпа учащихся выходит и ждет автобус, чтобы доехать до дома.) В любом случае, автобус может застрять в любой точке маршрута.
Если подумать об этом, то становится понятно, почему автобусы могут подъезжать по несколько штук. Когда одному автобусу приходится долго ждать, пока все пассажиры сядут, например, некоторые садятся медленнее, чем остальные, или группа ждущих пассажиров сама по себе большая, то увеличивается время, за которое автобус доедет до следующей остановки для сбора пассажиров, а значит, их станет больше. Потом когда автобус наконец приезжает на эту следующую остановку, все эти люди еще дольше садятся в автобус, а это значит, что на следующей остановке также будет больше людей. Этот процесс в сущности только становится хуже.
В это время автобус, который едет за отстающим автобусом, подъезжает на остановку и видит, что там его ждет очень мало пассажиров. Это потому, что большая часть уехала на предыдущем автобусе (отстающем). Так как ждущих пассажиров меньше, автобусу не надо долго ждать, пока все в него сядут. Поэтому он может трогаться сравнительно быстро, тем самым уменьшается время до прибытия на следующую остановку. И пока отстающий автобус едет все медленнее и медленнее, следующий автобус едет все быстрее и быстрее. В конце концов, этот автобус догоняет отстающий автобус, и они оба продолжают ехать по маршруту вместе (если только отстающий автобус не решит проезжать остановки, чтобы увеличить расстояние между ними).
Скопление автобусов – это пример теории хаоса, раздела математики, который изучает, как небольшие изменения при первоначальных условиях могут привести к непредсказуемым результатам в конечном итоге. В этом случае небольшие изменения во времени, которое люди тратят на посадку в автобус, значительно влияют на позицию автобуса в сравнении с другими автобусами этого маршрута.
Читать дальшеИнтервал:
Закладка:










