Павел Полуэктов - Озадачник: 133 вопроса на знание логики, математики и физики

Чему равняется произведение 748 × 1503?

1. 1 096 124.

2. 1 124 244.

3. 1 244 124.

Казалось бы, что может быть интересного в перемножении двух чисел? Берешь калькулятор и считаешь. Но с калькулятором и правда ничего интересного – иное дело попробовать посчитать в уме. Со всеми такими задачами главное – считать не в лоб, а попытаться увидеть, как можно облегчить себе работу. В конкретном нашем примере запишем 748 как (1500 – 4)/2, а 1503 как (1500 + 4) – 1, тогда получим: 748 × 1503 = (1500 – 4) (1500 + 4)/2 – 748. Вспоминая, что ( a – b ) × ( a + b ) = a ² – b ², получаем: 748 × 1503 = 1500²/2 – 4²/2 – 748 = 2 250 000/2 – 756 = 1 125 000–756 = 1 124 244. Возможность посчитать в уме (хотя бы приближенно, не всегда нужна совершенная точность) – очень важный навык. Знаменитый физик Ричард Фейнман посвятил этому целую главу в своей книге «Вы, конечно, шутите, мистер Фейнман!» [8], там он вычисляет в уме не только произведения, но и логарифмы, и кубические корни.

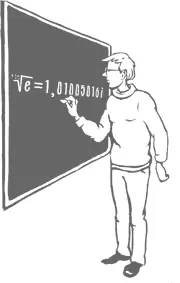
С точностью до третьей значащей цифры посчитайте в уме корень 100-й степени из числа e ( e = 2,718281828… – основание натурального логарифма). Это будет:

1. 1,01.

2. 1,04.

3. 1,11.

Чтобы решить эту задачку, нужно помнить две вещи. Первое: извлечь корень n -й степени – то же самое, что возвести в степень 1/ n , √ n ( a ) = a 1/n, в нашем случае нужно отыскать значение e в степени 1/100 = 0,01. Второе: при малых значениях аргумента функция e x(экспоненциальная функция, фундаментальная в математике – встречается без малого везде) может быть приближенно записана совсем просто: e x≈ 1 + x . Значит, искомое значение составит 1 + 0,01 = 1,01. Сравним с более точным (до 10-го знака) значением – это 1,010050167, великолепное совпадение! Приближенные методы, вообще, бывают довольно точны (главное контролировать эту точность). Скажем, корень десятой степени из e равен 1,105170918, а вычисленный по нашей приближенной формуле – 1,1, разница в полпроцента. Правда, если мы посчитаем e 1(равно e, если считать точно, и 2 по нашей формуле), то разница будет уже ощутимой, что объяснимо: для таких больших значений x наше приближение уже плохо работает, увы. Но его можно продолжать уточнять, почитайте, если интересно, про разложение экспоненты в ряд Тейлора, вы узнаете, что при любом (sic!) значении x , даже при миллионе или миллиарде, можно приближенно записать эту функцию полиномом (степенной функцией) с желаемой точностью!

В уме возвести 2 в 18-ю степень. Это:

1. 256 256.

2. 258 724.

3. 262 144.

Любой программист (а нынче и простой пользователь электронных гаджетов, который, например, изучал надписи на карте памяти и узнал, что 1 Гб – это вовсе не 1000 Мб, а 1024) знает, сколько будет 2 10 – чуть больше тысячи, точнее, те самые 1024. А 2 20 – соответственно 1024 × 1024. Но как это поможет вычислить 2 18? Очень просто: 2 18= 2 20∕ 2 2= 1024 × 1024 ∕ 2 × 2 = 512 × 512. А это уже совсем просто посчитать, вспомнив, что ( a + b ) × ( a + b ) = a ² + 2 ab + b ² (сравните с задачей № 41). Применительно к нашему примеру (500 + 12) × (500 + 12) = 500² + 2 × 12 × 500 + 12² = 250 000 + 12 000 + 144 = 262 144.

Что больше – десять в пятой степени или пять в десятой?

1. 10 5> 5 10.

2. 5 10> 10 5.

3. Возможно, они равны?

Сколько будет 10 5, мы, конечно же, знаем – это единица с пятью нулями, 100 000. А 5 10? На самом деле, вооружившись знаниями из предыдущего примера (№ 43), мы тоже легко можем посчитать, хотя бы приблизительно. Заметив, что 5 = 10/2, возведем последнюю дробь в десятую степень, помня правило возведения дроби в степень (числитель и знаменатель можно возводить в нее порознь), получим 10 10/2 10, а поскольку 2 10, как мы теперь уже знаем, это примерно 1000, т. е. 10³, получаем 5 10≈ 10 10/10 3= 10 7= 10 000 000. Значит, пять в десятой степени почти в 100 раз больше, чем десять в пятой! Интересно решить более общую задачу: если m > n , всегда ли, как в этом случае, n mбольше, чем m n? Оказывается, если и m , и n больше двойки (3, 4, 5 и т. д.), то да, всегда. А вот когда n = 2, есть два интересных случая: когда m = 3, 2³ (8) меньше, чем 3² (9), а когда m = 4, то 2 4и 4 2и вовсе равны (это 16). Если же m равно 5, 6 и т. д., мы снова возвращаемся к общему правилу 2 m> m ².

У Саши сестер на двое больше, чем братьев. На сколько у Сашиных родителей больше дочерей, чем сыновей?

1. На одну.

2. На три.

3. Невозможно определить.

Предположим для простоты, что у Саши две сестры и вовсе нет братьев. Тогда дочерей у Сашиных родителей на три больше, чем сыновей, если Саша девочка, и на одну, если он мальчик. Поскольку Саша – имя универсальное, может быть как мужским, так и женским, пол Саши определить не представляется возможным, как и ответить на поставленный в задаче вопрос.

В бассейне плавает глыба льда. Через некоторое время она тает. Что случилось с уровнем воды в бассейне?

1. Повысился.

2. Понизился.

3. Остался неизменным.

Уровень воды, разумеется, не изменится, и это очень легко объяснить наглядно. Поместим льдину в бесконечно легкую кастрюлю и пустим плавать в нашем бассейне. Льдина растаяла, но, так как масса содержимого кастрюли не изменилась, не изменился и уровень воды в бассейне. При этом, очевидно, уровень воды внутри (после таяния льда) и снаружи кастрюли (раз она не имеет массы) обязаны совпадать. Мысленно удаляем нашу воображаемую кастрюлю – вуаля, наше предположение доказано. Привет сторонникам теории глобального потепления.