Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Я знаю, как обычные люди воспринимают мою профессию: унылая тирания жестких правил и формульных процедур, где не больше разнообразия, чем, скажем, в заполнении страхового свидетельства или налоговой декларации. Вот пример задачки, которая ассоциируется с математикой:

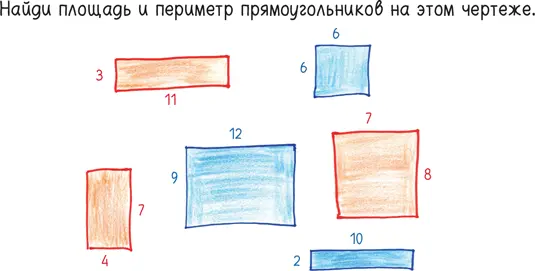
Эта задачка, вероятно, сможет занять ваше внимание на пару минут, хотя вскоре вы абстрагируетесь от геометрического смысла. Периметр больше не будет означать длину линии, ограничивающей прямоугольник. Он превратится просто-напросто в удвоенную сумму двух чисел. Как и в обычных крестиках-ноликах, все сведется к примитивным вычислениям, не требующим интеллектуального напряжения. Здесь нет места фантазии, нет вызова вашим способностям.

Но математика не ограничивается бухгалтерскими вычислениями, ее потенциал гораздо шире. Математика может быть дерзкой и увлекательной, успех может зависеть от баланса терпеливости и авантюризма. Попробуем переформулировать рутинную задачу, приведенную выше, в таком духе:

Эта задачка уже по-настоящему захватывающая. Она противопоставляет площадь и периметр. Вы не просто пользуетесь формулой; в процессе решения вам необходимо постичь суть прямоугольника. (Спойлеры — в примечаниях [4] Ключевая идея заключается в том, что у продолговатых прямоугольников непропорционально большой периметр, а у похожих на квадраты — непропорционально большая площадь. Поэтому нужно просто взять продолговатый прямоугольник (например, 10×1) и почти квадратный (например, 3×4). .)

Или как насчет такого:

В этом уже есть какая-то перчинка, не правда ли?

За два быстрых шага мы перескочили от сомнамбулически нудной работы к довольно любопытной небольшой головоломке, и у шестиклассников горят глаза, когда я закидываю им эту задачу в качестве дополнительного вопроса на итоговом экзамене. (Ответ — опять-таки в примечаниях [5] Если в ответе должны быть целые числа, задача становится еще веселее. Вот мой вывод формулы, порождающей целое семейство решений: Решений бесконечно много, но некоторые все равно остаются вне поля зрения, потому что другие значения d тоже могут давать целочисленные значения c . Например, эта формула не дает моего любимого решения: 1 × 33 и 11 × 6. Мой коллега Тим Кросс, съевший собаку на диофантовых уравнениях, подсказал мне ловкий способ найти все целочисленные решения. Моей профессии свойственна мизантропия, поэтому на сей раз я предлагаю читателю найти этот способ самостоятельно. .)

Творчество требует свободы, но одной свободы недостаточно. Псевдоголоволомка «нарисуйте два прямоугольника» подразумевает не только свободу, но и неизбежность скучных математических вычислений. Головоломка должна быть непредсказуемой, чтобы вызвать настоящий творческий порыв.

Вернемся к жестким крестикам-ноликам. У вас есть всего несколько вариантов каждого хода — вероятно, три или четыре. Их достаточно, чтобы включилось ваше воображение, и не настолько много, чтобы вы захлебнулись в море бессчетных альтернатив. Игра представляет собой гармонию жестких правил и свободы выбора.

И это великолепная иллюстрация того удовольствия, которое доставляет математика: творчество, порожденное непредсказуемостью. Привычные крестики-нолики — это математика с точки зрения большинства людей; жесткие крестики-нолики — это математика, какой она должна быть.

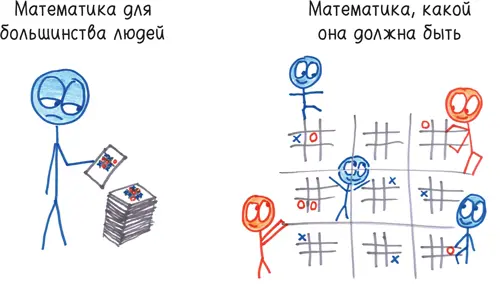
Вы можете найти множество аргументов в пользу того, что все творческие порывы стремятся нарушить четкие правила. По словам физика Ричарда Фейнмана, «творчество — это воображение в надежной смирительной рубашке». Жесткие правила сонета — «Укладывайся в ритм! Соблюдай длину строки! Следи за рифмовкой! Окей… а теперь выражай свою любовь, Вильям ты наш Шекспир!» — не ограничивают, а совершенствуют мастерство. Или возьмем, к примеру, спорт. Футболисты должны достичь определенной цели (забить мяч в ворота) , следуя твердым правилам (нельзя дотрагиваться до мяча руками) . В процессе игры они изобретают удар «ножницами» (удар через себя в падении) или удар «рыбкой» (удар головой в падении). Пренебрегая правилами, вы теряете изящество. Даже авангардное искусство — экспериментальный фильм, экспрессионистская картина, профессиональный реслинг — обретают силу благодаря тому, что выбор средств самовыражения ограничен.

Математики делают еще один концептуальный шаг. Мы не просто следуем заранее заданным правилам — мы изобретаем их и заигрываем с ними. Мы делаем предположение, выводим его логические следствия — и если они ведут в никуда или, что гораздо хуже, если они наводят скуку, мы ищем новый и более плодотворный путь.

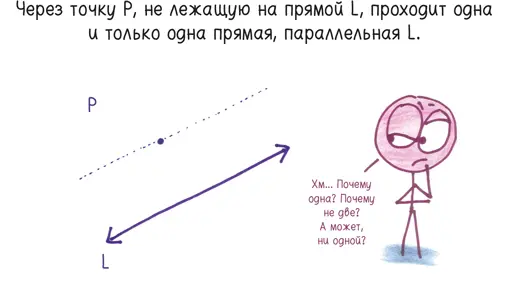
Например, что произойдет, если я усомнюсь в постулате о параллельных прямых?

Евклид изложил этот закон параллельных прямых примерно в 300 году до н. э.; он принял его как должное и назвал фундаментальным предположением («постулатом»). Его преемники сочли это несколько смехотворным. Мы действительно должны принимать на веру данное утверждение? Может быть, его можно доказать? На протяжении двух тысячелетий ученые ковыряли это правило, как волоконце мяса, застрявшее между зубов. В конце концов они поняли: «О да! Это всего лишь предположение». Вы можете предположить иное. В таком случае традиционная геометрия обрушится и уступит место диковинным альтернативным геометриям, где слова «параллельность» и «прямая» имеют совершенно другой смысл.

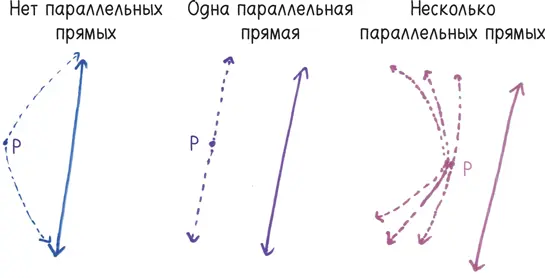
Новое правило — новая игра.

То же самое работает в случае с жесткими крестиками-ноликами. Вскоре после того, как я стал пропагандировать эту игру, я увидел единственную техническую деталь, на которой все держится. Она сводится к вопросу, которого я уже касался раньше. Как быть в том случае, если мой противник перенаправляет меня на мини-поле, которое уже сыграно?

Сейчас мой ответ совпадает с тем, который я приводил выше. Если мини-поле уже сыграно, вы можете выбрать любое другое.

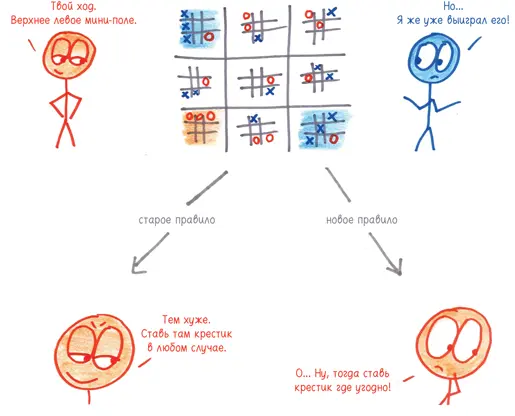
Но изначально мой ответ был другим. До тех пор, пока на этом мини-поле остаются пустые клетки, вам необходимо идти туда и делать ход, даже если он лишен смысла.