Крис Уоринг - Формулы на все случаи жизни. Как математика помогает выходить из сложных ситуаций

Переводчик Анна Туровская

Научный редактор Владислав Турченко

Редактор Любовь Макарина

Главный редактор С. Турко

Руководитель проекта О. Равданис

Арт-директор Ю. Буга

Адаптация оригинальной обложки Д. Изотов

Корректор А. Кондратова

Компьютерная верстка М. Поташкин

© Michael O'Mara Books Limited 2020

© Издание на русском языке, перевод, оформление. ООО «Альпина Паблишер», 2022

Все права защищены. Данная электронная книга предназначена исключительно для частного использования в личных (некоммерческих) целях. Электронная книга, ее части, фрагменты и элементы, включая текст, изображения и иное, не подлежат копированию и любому другому использованию без разрешения правообладателя. В частности, запрещено такое использование, в результате которого электронная книга, ее часть, фрагмент или элемент станут доступными ограниченному или неопределенному кругу лиц, в том числе посредством сети интернет, независимо от того, будет предоставляться доступ за плату или безвозмездно.

Копирование, воспроизведение и иное использование электронной книги, ее частей, фрагментов и элементов, выходящее за пределы частного использования в личных (некоммерческих) целях, без согласия правообладателя является незаконным и влечет уголовную, административную и гражданскую ответственность.

Уравнения и формулы. Большинству из нас они знакомы по школьным урокам математики, физики и химии. Но, вероятнее всего, даже те из них, что были некогда вызубрены для экзаменов, теперь пылятся где-то на задворках нашего взрослого разума – позабытые и, казалось бы, совершенно ненужные. В конце концов, нам действительно чаще всего требуются простейшие арифметические действия, а в самом крайнем случае (скажем, за неделю до зарплаты) – умение пользоваться калькулятором на смартфоне. Так зачем возвращаться к этим никчемным, бесполезным, никому не нужным штукам, если для задачи, которая внезапно потребовала решения, уже наверняка придумали приложение, электронную таблицу или программу?

Насколько мы можем судить, наша Вселенная подчиняется неким законам. Мы называем эти законы наукой и записываем математическим языком – при помощи уравнений. Абсолютно все – от образования галактик до расположения веснушек на носу ребенка – есть результат решения уравнений. Нравится вам это или нет, предпочитаете ли вы «метод научного тыка» или упорядоченные действия – уравнения сопровождают каждый аспект вашей жизни. Совершенно неважно, насколько решение уравнений доступно вашему пониманию – они управляют всем, что происходит вокруг. Так может быть, пора поближе познакомиться с миром математики?

Безусловно, уравнения помогут вычислить, какой дистанции следует придерживаться, чтобы избежать столкновения машин в час пик. Но они могут оказаться полезными и в чрезвычайных обстоятельствах – когда на кону стоит больше, чем выплата по страховке. Что, если вместо того, чтобы поутру тащиться на скучную работу в офис мистера Претенциозность, вы перехватываете сообщение от обитателей другой галактики? Или, останавливая чудовищный разлив нефти в Тихом океане, предупреждаете международный конфликт? В старом добром уравнении нуждаются даже важные для всех и шаткие с точки зрения международной дипломатии ситуации. Математика – то, что движет миром, а совершенствование математических знаний – то, что поможет развитию технологий и, возможно, спасет планету от экологической катастрофы!

Однако прежде, чем приняться за спасение жизней, давайте вспомним основы математики. Они понадобятся, если вы хотите читать эту книгу хоть сколько-нибудь осознанно.

Любому из нас, бывает, требуется помощь с математикой. Даже такие гении, как Исаак Ньютон и Альберт Эйнштейн, время от времени затруднялись записывать свои теории математическим языком и обращались за помощью к экспертам. Я не смогу быть рядом и помогать, пока вы читаете. Но я написал несколько пояснений: они облегчат понимание тех вещей, которые вы, возможно, успели подзабыть со школьных времен. Уверены в собственных знаниях – пропускайте этот раздел. К нему можно будет вернуться, если вдруг поймете, что переоценили свои способности.

Всякий раз, когда вы видите выражение, требующее вычислений – или операций, как это называют математики, – вам нужно определить последовательность шагов. В отличие от письма или чтения, где мы движемся слева направо, в математике необходимо следовать определенному порядку.

Вычисления следует производить согласно аббревиатуре BIDMAS [1] Аббревиатура BIDMAS происходит от принятой в математике последовательности операций: brackets (скобки), indices (степени), division (деление), multiplication (умножение), addition (сложение), subtraction (вычитание). – Прим. пер. :

Скобки

Возведение в степень

Деление

Умножение

Сложение

Вычитание

Например, выражение 5 – 3 + (2 × 8) ÷ 4 2содержит все шесть действий. Итак, начнем со скобок. Мы видим, что 2 × 8 = 16, и наш пример становится таким:

5 – 3 + 16 ÷ 4 2.

Далее по плану возведение в степень («в степени n» означает «в n раз больше»). Такую степень мы видим над числом 4. 4 2 – это число 4, умноженное само на себя. Поскольку 4 × 4 = 16, мы получаем:

5 – 3 + 16 ÷ 16.

Затем идет деление: 16 ÷ 16 = 1. Теперь наше выражение принимает вид:

5 – 3 + 1.

Сложение –3 и 1 дает нам –2:

5 – 2.

У нас на руках остается простое вычитание:

5 – 2 = 3.

Эквивалентность дробей – важное понятие: это означает, что дроби, пусть и записанные по-разному, могут соответствовать одному и тому же числу. Например, как мы знаем, одна вторая – то же самое, что и две четверти:

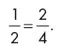
Дроби принято оставлять в несократимом виде, то есть использовать наименьший возможный знаменатель (число под чертой) при целом числителе (число над чертой). Будь нам неизвестно, что две четверти эквивалентны половине, мы могли бы сократить дробь, найдя число, которому кратны и числитель, и знаменатель. Для двух четвертей оно будет равно двум, так как на него делятся и 2, и 4. Поделив оба числа на 2, мы сократим дробь, но ее значение останется таким же.

Если бы у нас было восемь двенадцатых, мы могли бы разделить числитель и знаменатель на 2 или на 4. Чтобы полностью сократить дробь, используем наибольший общий делитель: