Ирина Краева - Квадратные уравнения. Часть 1

Таким образом, отсутствие в записи конкретного уравнения свободного члена или слагаемого с первой степенью неизвестного не даёт нам права сомневаться в том, что уравнение всё-таки квадратное. Однако и наличие их не является веской причиной отнести уравнение к квадратным. Об этом чуть ниже.

Следующим возникает вопрос, а почему, собственно a ≠ 0? (Конечно, искушённый читатель знает почему.) Можно ли, например, уравнение вида ax 2 + ( a – 1) x + a = 0 (или в общем виде f ( a ) x 2 + g ( a ) x + h ( a ) = 0) называть квадратным?

Давайте похулиганим и поставим в качестве первого коэффициента ноль. Тогда уравнение примет вид bx + c = 0.

Но это же линейное уравнение! Оно имеет свою теорию, свои изюминки.

Пусть будут «мухи отдельно, котлеты отдельно».

Теперь понятно, что требование a ≠ 0 необходимо для сохранения в квадратном уравнении второй степени – квадрата – неизвестного. Вот этот признак будет определяющим!

В дальнейшем, говоря о квадратном уравнении, мы будем помнить, что старший коэффициент не равен нулю, не оговаривая это каждый раз. Договорились?

Тогда уравнение f ( a ) x 2 + g ( a ) x + h ( a ) = 0 правильно называть уравнением с параметром второй степени , которое при определённых условиях может быть квадратным, а может им и не быть (стать линейным).

Однако не будем торопиться. Наличие второй степени неизвестного – необходимый, но не достаточный признак квадратного уравнения.

Рассмотрим следующие уравнения:

Выполним сравнительный анализ этих уравнений с квадратным ax 2 + bx + c = 0 по трём признакам:

– наличие второй степени неизвестной,

– наибольшая степень неизвестной,

– количество неизвестных.

Зафиксируем для каждого уравнения эти параметры.

Результаты сравнительного анализа организуем в таблицу.

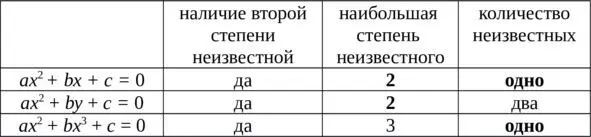
Итак, что мы имеем?

Наличие второй степени неизвестного является общим для всех трёх уравнений. Но по двум другим признакам сравнения, квадратное уравнение отличается: в квадратном уравнении вторая степень неизвестной является наибольшей и неизвестная только одна.

Именно это и важно!

Собственно говоря, квадратным является целое рациональное (или по-другому – алгебраическое) уравнение второй степени с одним неизвестным 2 2 Подробнее смотрите в приложении. .

Процесс ограничения класса алгебраических уравнений можно представить в двух направлениях:

алгебраическое уравнение → первой степени, второй степени и так далее;

алгебраическое уравнение → с одной неизвестной, с двумя неизвестными и так далее.

Приведём примеры:

ax + b = 0 – уравнение первой степени с одной неизвестной;

ax + by + c = 0 – уравнение первой степени с двумя неизвестными;

ax 2 + bx + c = 0 – уравнение второй степени с одной неизвестной;

ax 2 + bxy + cy 2 + kx + ly + m = 0 – уравнение второй степени с двумя неизвестными.

Тогда ближайшими родовыми понятиями для квадратного уравнения будут: алгебраическое уравнение второй степени или алгебраическое уравнение с одним неизвестным. Выбирая в качестве родового понятия разные объекты, мы сможем получить различные формулировки определения квадратного уравнения. Попробуйте!

Наконец, рассмотрим правую часть равенства в определении квадратного уравнения. Она представляет собой конкретное число – ноль. А может быть что-нибудь другое?

Если мы хотим видеть квадратное уравнение «в чистом виде», то ничего, кроме нуля, в правой части быть не должно. Но…

Рассмотрим уравнение ax 2 + bx + c = m , где m число отличное от нуля. Тогда мы, основываясь на равносильности преобразований уравнений 3 3 О равносильности опять же смотри приложение. , можем записать

ax 2 + bx + c – m = 0

ax 2 + bx + ( c – m ) = 0

ax 2 + bx + c 1 = 0.

То есть мы, собственно, получили квадратное уравнение.

Ещё пример:

ax 2 + bx + c = mx + n

ax 2 + bx + c — mx – n = 0

ax 2 + bx – mx + c – n = 0

ax 2 + ( b – m ) x + ( c – n ) = 0

ax 2 + b 1 x + c 1 = 0.

Таким образом, уравнения двух приведённых выше видов

ax 2 + bx + c = m и ax 2 + bx + c = mx + n есть смысл назвать сводящимися к квадратным. То есть, если в правой части стоит многочлен с одной (той же, что и в левой части!) неизвестной степени не выше первой, то с помощью соответствующих преобразований квадратное уравнение мы получим без проблем.

Если же в правой части будет стоять многочлен с одной неизвестной второй степени, то квадратное уравнение может и не получиться.

Ситуация первая: ax 2 + bx + c =ay 2 + by + c.

Как бы ни старались, квадратного уравнения мы не получим. Неизвестных две, и это равенство не входит в множество математических объектов «квадратные уравнения». Вывод: неизвестная правой части должна быть такой же, что и в левой!

Ситуация вторая. Преобразуйте самостоятельно, например, два следующих уравнения:

ax 2 + bx + c = kx 2 + mx + n

ax 2 + bx + c = ax 2 + mx + n .

Получилось ли у вас квадратное уравнение в первом случае? А во втором? Как будет называться уравнение, которое сведётся не к квадратному?

Определите условие, при котором уравнение такого вида всё-таки будет сводиться к квадратному 4 4 В конце книги есть раздел «Комментарии». Можете сверить свои идеи и мысли. .

Как ещё один пример рассмотрите уравнение

x 2 – 9 = ( x – 5) ( x +7).

Таким образом, наличие второй степени неизвестной в записи уравнения не всегда будет означать, что оно квадратное.