Морис Клайн - Математика. Утрата определенности.

Ньютон принял гипотезу, высказанную его предшественниками, а именно: он предположил, что сила F взаимного притяжения любых двух тел с массами m и M, удаленных друг от друга на расстояние r, выражается формулой (1):

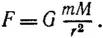
В этой формуле G — постоянная, т.е. имеет одно и то же значение при любых m, M и r. Значение этой постоянной зависит от того, в каких единицах измеряются масса, сила и расстояние. Ньютон обобщил также установленные Галилеем законы движения земных тел. Эти обобщения известны под названием трех законов Ньютона. Первый закон Ньютона, сформулированный еще Декартом и Галилеем, гласит: «Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного прямолинейного движения, пока и поскольку оно не принуждается приложенными силами изменить это состояние». Второй закон утверждает, что «изменение количества движения пропорционально приложенной движущей силе и происходит по той прямой, по которой эта сила действует». Согласно третьему закону, «действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны» ([20], с. 39-41). Опираясь на три закона движения и закон всемирного тяготения (1), Ньютон получил возможность описывать движения земных тел.

В теории движения небесных тел Ньютон одержал блестящую победу, доказав, что три закона Кеплера, полученные им методом проб и ошибок на основании результатов многолетних наблюдений Тихо Браге, представляют собой не что иное, как математические следствия из закона всемирного тяготения и трех законов движения. Тем самым Ньютон показал, что движение планет, которое, как полагали до него, не имеет ничего общего с движением земных тел, в действительности подчиняется тем же законам, что и движение земных тел. В этом смысле Ньютон «объяснил» законы движения планет. Кроме того, поскольку законы Кеплера согласуются с результатами наблюдений, их вывод из закона всемирного тяготения стал превосходным подтверждением правильности самого этого закона.

Те немногие следствия из законов движения и закона всемирного тяготения, о которых мы упомянули, — всего лишь небольшой пример того, что было дано свершить Ньютону. Закон всемирного тяготения он применил к объяснению непонятного ранее явления — океанских приливов. Их вызывают силы притяжения, действующие со стороны Луны и в меньшей степени со стороны Солнца на большие массы воды. По данным о высоте лунных приливов (приливов, вызываемых притяжением Луны) Ньютон вычислил массу Луны. Ньютон и Гюйгенс оценили величину экваториального утолщения Земли. Ньютон и другие показали, что движение комет также согласуется с законом всемирного тяготения. Тем самым кометы были признаны законными членами Солнечной системы; их перестали считать случайными пришельцами из космических глубин или знамениями, сулящими грозную кару и гибель. Ньютон показал, что вследствие экваториального утолщения Земли земная ось под действием притяжения Луны и Солнца не указывает неизменно на одну и ту же звезду, а описывает конус с периодом 26 000 лет. Это долгопериодическое изменение направления земной оси приводит ежегодно к небольшим сдвигам в наступлении весеннего и осеннего равноденствий, отмеченным Гиппархом за 1800 лет до Ньютона. Так Ньютон объяснил смещение равноденствий.

Наконец, используя приближенные методы, Ньютон решил некоторые задачи, относящиеся к движению Луны. Например, известно, что плоскость, в которой происходит движение Луны, несколько наклонена к плоскости движения Земли. Как показал Ньютон, это обусловлено взаимным притяжением Солнца, Земли и Луны, описываемым законом всемирного тяготения. Ньютон и его непосредственные преемники в науке вывели из закона всемирного тяготения так много важных следствий о движениях планет, комет и Луны, а также о колебаниях уровня моря, что на протяжении последующих двух столетий считалось, что они дали полное объяснение системы мира.

В своей грандиозной деятельности Ньютон придерживался принципа, выдвинутого Галилеем, — искать не физическое объяснение, а математическое описание. Ньютон не только свел воедино огромное число экспериментальных данных и теоретических результатов Кеплера, Галилея и Гюйгенса, но и поставил математическое описание в основу всех своих естественнонаучных трудов и предсказаний. В предисловии к первому изданию своего основного труда, носившего весьма примечательное название «Математические начала натуральной философии» {30}, Ньютон говорит:

Так как древние, по словам Паппуса, придавали большое значение механике при изучении природы, то новейшие авторы, отбросив субстанции и скрытые свойства, стараются подчинить явления природы законам математики.

В этом сочинении имеется в виду тщательное развитие приложений математики к физике, поэтому и сочинение это нами предлагается как математические основания физики. Вся трудность физики, как будет видно, состоит в том, чтобы по явлениям движения распознать силы природы, а затем по этим силам объяснить остальные явления. Для этой цели предназначены общие предложения, изложенные в книгах первой и второй. Затем по этим силам, также при помощи математических предложений, выводятся движения планет, комет, Луны и моря.

Мы видим, что математике в «Началах» Ньютона отводится главная роль.

У Ньютона имелись все основания отдавать количественным математическим законам предпочтение перед физическим объяснением: центральным физическим понятием ньютоновской небесной механики была сила тяготения, а действие этой силы он не мог объяснить с помощью физических понятий. Представление о силе тяготения, действующей между любыми двумя массами, даже если их разделяют сотни миллионов километров пустого пространства, казалось столь же невероятным, как и многие свойства, придуманные для объяснения физических явлений последователями Аристотеля и средневековыми схоластами. Представление о дальнодействующих силах было особенно неприемлемым для современников Ньютона, упорно настаивавших на механистических объяснениях и привыкших воспринимать силу как результат непосредственного соприкосновения тел, при котором одно тело «толкает» другое. {31}Отказ от физического объяснения и прямая замена его математическим описанием явления потрясли даже великих ученых. Гюйгенс считал идею гравитации «абсурдом», поскольку действие через пустое пространство исключало всякий механизм передачи силы; он поражался тем, что Ньютон взял на себя тяжкий труд и выполнил громоздкие вычисления, которые не обосновывались — ничем, кроме математического принципа тяготения. Против чисто математического описания гравитации возражали и многие другие современники Ньютона, в том числе Лейбниц, который сразу, как только прочитал в 1690 г. ньютоновские «Начала», занял в отношении их резко критическую позицию и продолжал критиковать идею дальнодействия до самой своей смерти. Вольтер, возвратившись в 1727 г. с похорон Ньютона, с иронией заметил, что в Лондоне царит вакуум, тогда как в Париже ощущается пленум (пространство, заполненное тончайшей материей) — ведь во Франции все еще царствовала картезианская философия. Попытки объяснения феномена дальнодействия не прекращались до начала XX в.