Морис Клайн - Математика. Поиск истины.

И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные эти две прямые неограниченно встречаются с той стороны, где углы меньше двух прямых.

Это означает (рис. 32), что если углы 1 и 2 в сумме меньше 180°, то прямые a и b , будучи продолженными достаточно далеко, пересекутся (на рисунке — справа).

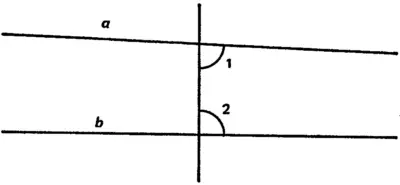
Рис. 32.

Евклид имел достаточно веские основания, чтобы сформулировать свою аксиому именно так. Он мог бы утверждать, что если сумма углов 1 и 2 равна 180°, то прямые a и b никогда не пересекутся, сколько бы их ни продолжали, т.е. что прямые a и b в этом случае параллельны. Однако Евклид явно опасался предположить, что могут существовать две бесконечные прямые, которые никогда не пересекаются. Существование таких прямых не подкреплялось опытом и отнюдь не было самоочевидным. Но на основе аксиомы о параллельных и других аксиом своей геометрии Евклид доказал существование бесконечно протяженных параллельных прямых.

Считалось, что аксиома о параллельных в том виде, в каком ее сформулировал Евклид, излишне сложна и ей недостает простоты других аксиом. Самого Евклида придуманный им вариант аксиомы о параллельных также не устраивал: недаром он обращался к этой аксиоме, лишь доказав все теоремы, какие только можно было доказать без нее.

Даже в античную эпоху математики неоднократно пытались решить проблему, связанную с аксиомой о параллельных Евклида. Эти попытки были двух типов. Одни пробовали заменить аксиому о параллельных какой-нибудь другой аксиомой, казавшейся им более очевидной. Другие старались, вывести аксиому Евклида из девяти других аксиом его геометрии. Если бы это удалось, то аксиома о параллельных превратилась бы в одну из теорем и всякие сомнения в ее истинности разом отпали бы. На протяжении двух тысячелетий не один десяток самых выдающихся математиков, не говоря уже о менее известных, пытались и заменить аксиому о параллельных и вывести ее из других аксиом. История аксиомы Евклида о параллельных длительна, изобилует техническими деталями, и мы не будем пересказывать ее здесь подробно, тем более что она не имеет прямого отношения к главной теме нашего повествования и неоднократно излагалась в других работах. {10}

Из аксиом, предлагавшихся взамен аксиомы Евклида о параллельных, нельзя не упомянуть по крайней мере одну. Мы остановили свой выбор на ней потому, что именно с такой редакцией аксиомы о параллельных мы обычно знакомимся в школьном курсе геометрии. Автором этого варианта аксиомы принято считать Джона Плейфера (1748-1819), который предложил его в 1795 г. Аксиома Плейфера гласит:

Существует одна и только одна прямая, проходящая через данную точку P , лежащую вне прямой l (рис. 33), в плоскости, задаваемой точкой P и прямой l , которая не пересекается с прямой l .

Все остальные аксиомы, предлагавшиеся взамен аксиомы Евклида о параллельных и казавшиеся на первый взгляд более простыми, чем первоначальный вариант, при более тщательном рассмотрении признавались менее удовлетворительными. Нельзя не заметить, что аксиома Плейфера утверждает именно то, чего стремился избежать Евклид: существование двух бесконечных прямых, которые никогда не пересекаются.

Среди попыток второго типа, которые выражались в намерении вывести аксиому о параллельных из девяти других аксиом Евклида, наиболее преуспел член ордена иезуитов, профессор университета в Павии Джероламо Саккери (1667-1733). Он рассуждал так. Если принять аксиому, существенно отличающуюся от аксиомы Евклида о параллельных, то можно было бы прийти к какой-нибудь теореме, которая противоречила бы другой теореме. Такое противоречие означало бы, что аксиома, отрицающая аксиому Евклида о параллельных — единственную сомнительную аксиому евклидовой геометрии, — ложна. Но тогда аксиома Евклида о параллельных должна была бы быть истинной, т.е. следствием, вытекающим из девяти других аксиом.

Как впоследствии Плейфер, предложивший аксиому, эквивалентную аксиоме Евклида, Саккери сначала предположил, что не существует прямых, параллельных прямой l , которые проходили бы через точку P , лежащую вне прямой l (рис. 33). Из этой аксиомы и девяти других аксиом Евклида Саккери действительно удалось вывести противоречие. Тогда Саккери испробовал вторую единственно возможную альтернативу, предположив, что существуют по крайней мере две прямые p и q , проходящие через точку P и не пересекающиеся с прямой l , сколько бы их ни продолжали.

Рис. 33.

Саккери доказал довольно много интересных теорем прежде, чем ему удалось обнаружить теорему, столь необычную и так резко выпадавшую из всего ранее известного, что он усмотрел было в ней противоречие с ранее доказанными утверждениями. Исходя из этого, Саккери счел доказанным, что аксиома Евклида о параллельных следует из девяти остальных аксиом евклидовой геометрии, и в 1773 г. опубликовал книгу под названием «Евклид, избавленный от всяких пятен» (Euclides ab omnia naevo vindicatus). Но как позднее установили математики, Саккери во втором случае не удалось прийти к противоречию, поэтому проблема, связанная с аксиомой о параллельных, по-прежнему оставалась открытой.

Попытки найти приемлемую замену евклидовой аксиомы о параллельных или доказать, что она должна следовать из девяти остальных аксиом Евклида, были столь многочисленны и столь безуспешны, что в 1759 г. выдающийся математик Жан Лерон Д'Аламбер (1717-1783) назвал проблему, связанную с аксиомой о параллельных, «скандалом оснований геометрии».

Постепенно у математиков начало складываться правильное понимание истинного статуса аксиомы Евклида о параллельных. В своей докторской диссертации (1763) Георг С. Клюгель (1739-1812), впоследствии профессор университета в Хальмстаде, высказал весьма глубокое замечание о том, что восприятие аксиомы Евклида о параллельных как чего-то достоверного основано на человеческом опыте. В этом замечании Клюгеля впервые прозвучала мысль о том, что аксиомы опираются не столько на очевидность, сколько на опыт. Клюгель выразил сомнение в том, что аксиома Евклида о параллельных доказуема, и понял, что Саккери пришел не к противоречию, а всего лишь к необычному результату.

Диссертация Клюгеля привлекла внимание Иогана Генриха Ламберта (1728-1777), побудив его также заняться аксиомой о параллельных. В своей книге «Теория параллельных прямых», написанной в 1766 г., а изданной в 1786 г., Ламберт, в какой-то мере следуя Саккери, рассмотрел две альтернативные возможности. Предположив, что через точку P , расположенную вне прямой l (см. рис. 33), не проходит ни одной прямой, параллельной l , он также пришел к противоречию. Но в отличие от Саккери Ламберт не считал, что предположение о существовании по крайней мере двух параллельных, проходящих через точку P , приводит к противоречию. Кроме того, Ламберт понял, что любая система аксиом, которая не приводит к противоречию, порождает свою геометрию. Любая такая геометрия логически ничему не противоречит, хотя и имеет весьма косвенное отношение к реальным физическим фигурам!