Морис Клайн - Математика. Поиск истины.

Два наблюдателя, движущиеся друг относительно друга равномерно и прямолинейно, разойдутся во мнениях не только при измерениях расстояний, но и при измерениях продолжительности промежутков времени. В противном случае наблюдатели должны были бы прийти к согласию относительно событий, отмечающих начало и конец временного интервала.

Но выводы, которые извлек из своих постулатов Эйнштейн, далеко не исчерпываются этим. Если один наблюдатель неподвижен, а другой движется относительно него с постоянной скоростью v в заданном направлении (как, например, наблюдатель в поезде), то длина отрезка в движущейся вместе со вторым наблюдателем системе отсчета по измерениям неподвижного наблюдателя окажется короче, чем по измерениям движущегося наблюдателя, и наоборот. Что касается времени, то неподвижному наблюдателю кажется, что наблюдатель, движущийся, например, относительно Земли, перемещается медленнее. Сигара движущегося наблюдателя кажется неподвижному наблюдателю короче, чем его собственная. Иначе говоря, часы в системе отсчета S' покоятся в этой системе. При наблюдении из другой системы отсчета S часы в системе отсчета S' замедляют свой ход на (1 − 1/β) за секунду, где β = √(1 − v 2/c 2) . Верно и обратное. В общем случае соотношение между двумя системами отсчета задается преобразованием Лоренца. Кроме того, невозможно отделить измерение пространства от измерения времени (если не считать наблюдателя, производящего измерения в своей собственной системе отсчета), подобно тому как мы не можем отделить одновременно для всех наблюдателей горизонтальное направление от вертикального.

Следует подчеркнуть, что, говоря о различии в результатах измерений длины, производимых различными наблюдателями, мы отнюдь не имеем в виду эффект влияния расстояния на их зрительное восприятие или какие-либо оптические иллюзии. Равным образом, говоря о расхождении в оценках наблюдателями продолжительности временных интервалов, мы никак не связываем это с психологическими или эмоциональными эффектами.

Рассмотрим численный пример. Наблюдателю на Земле космический корабль, летящий с околосветовой скоростью 270 000 км/с относительно Земли, покажется вдвое короче, чем наблюдателю на борту корабля. Часы, находящиеся на борту этого космического корабля, будут казаться земному наблюдателю идущими вдвое медленнее, чем наблюдателю на борту космического корабля. К аналогичным заключениям наблюдатель, находящийся на борту космического корабля, придет относительно размеров объектов и продолжительности событий на Земле. Более того, каждый набор измерений правилен, но в своем собственном пространстве и времени.

В концепции локальной длины и локального времени заключается одно из принципиально новых положений специальной теории относительности. Их необычность не должна скрывать от нас то, что они гораздо лучше согласуются с экспериментом и приведенными выше рассуждениями по поводу одновременности событий, чем ньютоновские понятия абсолютного пространства и времени. Впрочем, если бы дело обстояло иначе, то, какими бы ни были понятия специальной теории относительности, относительными или абсолютными, никто из ученых не стал бы их придерживаться. Соотношения между длиной и продолжительностью временного интервала, измеряемыми одним наблюдателем, движущимся относительно другого равномерно и прямолинейно со скоростью v , могут быть выведены из преобразования Лоренца.

Еще одно следствие из постулатов специальной теории относительности касается сложения скоростей. Предположим, что в стоячей воде лодка движется со скоростью 6 км/ч, а скорость течения равна 2 км/ч. Можно ли утверждать, что вниз по течению лодка будет плыть со скоростью 8 км/ч? Нет, специальная теория относительности приводит к иному ответу. Скорость V , при сложении скоростей u и v определяется по формуле

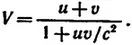
Небезынтересно отметить одно следствие из этой формулы: если u = c , то V = c .

Но, возможно, самое необычное следствие специальной теории относительности касается массы движущегося тела; оно гласит, что масса любого объекта увеличивается со скоростью. Зависимость массы от скорости Эйнштейн рассмотрел в четвертой из своих статей, опубликованных в 1905 г. Если m — масса тела, покоящегося относительно наблюдателя, а M — масса того же тела, движущегося со скоростью v относительно наблюдателя, то они связаны зависимостью (1):

Возможно ли подобное? Ведь когда скорость тела возрастает, число молекул в нем отнюдь не увеличивается. Ответ на этот вопрос поистине удивителен. Можно показать, что с вполне удовлетворительной точностью приращение массы тела равно кинетической энергии его массы покоя, деленной на c 2 . Грубо говоря, приращение массы тела эквивалентно его кинетической энергии. Можно сказать, что движущаяся масса ведет себя так, как будто она увеличивается, но физически это увеличение сводится к энергии тела.

Хотя взаимосвязь массы и энергии на первый взгляд может показаться невероятной, на самом деле мы сталкиваемся с этим в повседневной жизни. Рассмотрим сначала явление превращения массы в энергию. Так, когда мы пользуемся карманным фонариком, мы по существу превращаем массу вещества, заключенного в батарейках, в световое излучение, обладающее определенной энергией. Свет может привести во вращение крыльчатку игрушечного радиометра. Ясно, что световое излучение обладает массой, которая, ударяясь о крылышки радиометра, заставляет их вращаться. Мы сжигаем мазут в отопительных системах, сжигаем бензин в моторах автомобилей, чтобы привести их в действие. И в том и в другом случае мы превращаем массу в энергию, как и сжигая дрова для обогрева своего жилища, ибо тепло — одна из форм энергии. Солнечный свет является основным источником энергии на Земле. Растения превращают его в химическую энергию. В процессе фотосинтеза, происходящего в листьях зеленых растений, энергия солнечного света поглощается и используется для превращения воды, диоксида углерода (углекислого газа) и минералов в органические соединения, богатые кислородом и энергией.

Эйнштейн высказал предположение, что увеличение массы можно было бы наблюдать на частицах, испускаемых при радиоактивном распаде, например на β- частицах (электронах), если разогнать их до высоких скоростей. Это предсказание Эйнштейна получило экспериментальное подтверждение. Нечто похожее происходит, когда мы нагреваем массу, тем самым подводя к ней энергию: масса увеличивается.

К счастью или несчастью, существует и обратный процесс. Частица вещества теряет часть своей массы, отдав соответствующее количество энергии. Частицу можно замедлить, вынуждая ее расходовать массу и тем самым энергию. К поистине трагическим последствиям может привести огромное количество энергии, выделяющейся в виде излучения при делении атомного ядра или при термоядерном синтезе (в первом случае суммарная масса осколков деления меньше массы исходного ядра, во втором — масса продуктов реакции меньше массы исходных частиц). В превращении образовавшегося «дефекта массы» в энергию и состоит принцип действия атомной и водородной бомб.