Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
- Название:Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
- Автор:
- Жанр:
- Издательство:Астрель: CORPUS
- Год:2010
- Город:Москва
- ISBN:978-5-271-25422-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. краткое содержание
Сколько имеется простых чисел, не превышающих 20? Их восемь: 2, 3, 5, 7, 11, 13, 17 и 19. А сколько простых чисел, не превышающих миллиона? Миллиарда? Существует ли общая формула, которая могла бы избавить нас от прямого пересчета? Догадка, выдвинутая по этому поводу немецким математиком Бернхардом Риманом в 1859 году, для многих поколений ученых стала навязчивой идеей: изящная, интуитивно понятная и при этом совершенно недоказуемая, она остается одной из величайших нерешенных задач в современной математике. Неслучайно Математический Институт Клея включил гипотезу Римана в число семи «проблем тысячелетия», за решение каждой из которых установлена награда в один миллион долларов. Популярная и остроумная книга американского математика и публициста Джона Дербишира рассказывает о многочисленных попытках доказать (или опровергнуть) гипотезу Римана, предпринимавшихся за последние сто пятьдесят лет, а также о судьбах людей, одержимых этой задачей.
Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Каждое из этих 13 слагаемых состоит из четырех членов: главный член, вторичный член (куда и входят нули дзета-функции), член с ln 2 и интегральный член. Если сложить все эти 52 куска, получится π (1000 000) — число, про которое мы заранее знаем из главы 3.iii, что оно равно 78 498.
Вся эта арифметика расписана в таблице 21.1 (там опущены строки с N , для которых J(N) равно нулю). Двигаясь вдоль строки N и используя y для обозначения N- го корня из одного миллиона, имеем главный член 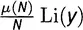 , вторичный член
, вторичный член 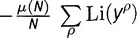 , член с ln 2, равный
, член с ln 2, равный 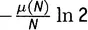 , и интегральный член
, и интегральный член 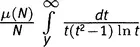 . Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
. Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
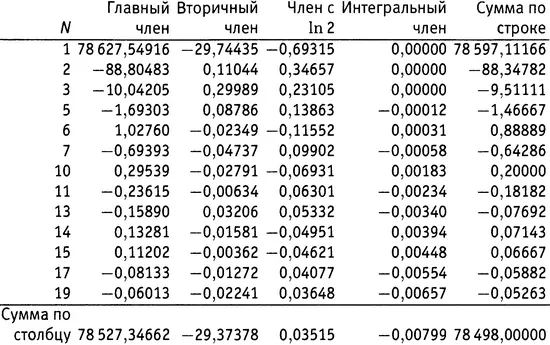
Таблица 21.1.Вычисление π (1000 000).
В качестве простой проверки возьмем строку с N = 6. Поскольку миллион — это 10 6, корень шестой степени из миллиона — это просто 10. Значение J (10) легко посчитать — оно оказывается равным 16/ 3. Поскольку число 10 свободно от квадратов и представляет собой произведение двух простых чисел, функция Мебиуса μ (10) имеет значение +1. Итак, в строке с N = 6 последний столбец должен быть равен (+1)×( 1/ 6)×( 16/ 3). Это составляет 8/ 9, что и говорится в суммарной колонке для строки с N = 6.
При N = 1 главный член, равен просто Li(1000 000); именно такое приближение к точному ответу дает нам ТРПЧ. Какова же разница между этим приближением и π (1000 000)? Ответ получается мгновенно путем простого вычитания: разность, вычисленная как π (1000 000) минус Li(1000 000) (чтобы сохранить знаки в нашей таблице), равна −129,54916. Из чего эта разница слагается?
Вот из чего:
| из главных членов | −100,20254 |
| из вторичных членов | −29,37378 |
| из членов с ln 2 | 0,03515 |
| из интегральных членов | −0,00799 |
Наибольший вклад в разницу дают главные члены. Однако эти члены вполне предсказуемы — они убывают быстро и неуклонно.
Разница, возникающая из вторичных членов, имеет тот же порядок величины, однако составляющие ее компоненты — те самые вторичные члены — вызывают куда больше беспокойства. Первый вторичный член достаточно велик и отрицателен; правда, нет никаких очевидных причин, почему он должен оказаться именно таким. Но и другие не очень помогают. Если просто двигаться вниз вдоль колонки с вторичными членами, не обращая внимания на знаки минус, а следя только за тем, будет ли каждый следующий член больше или меньше предыдущего по величине, то мы увидим такое: меньше, больше, меньше, меньше, больше, меньше, меньше, больше, меньше, меньше, больше, больше. Вторичный член при N = 19 оказывается почти таким же, как и при N = 6. Все эти вторичные члены — члены, которые выражаются через нули дзета-функции, — джокеры в нашем вычислении. А члены с ln 2, как и было обещано, несущественны.
Вспомним о статье Литлвуда 1914 года (см. главу 14.vii), где он доказал, что неверно утверждение, что Li (x) всегда превосходит π(x) . Это означает, что разность рано или поздно станет положительной. Поскольку главные члены очень быстро убывают по величине, а функция Мебиуса делает несколько первых из них отрицательными, включая и по-настоящему большие (при N = 2, N = 3 и N = 5), нелегко представить себе, как же эти главные члены вообще могут внести в разность какой-нибудь иной вклад, кроме как большое отрицательное число. Если в итоге разность должна оказаться положительной (а Литлвуд доказал, что такое рано или поздно случится), то это отрицательное число должно поглотиться большими, положительными, вторичными членами. Чтобы такое произошло, вторичные члены — нули дзета-функции — должны серьезным образом выйти из-под контроля. Судя по всему, так они и делают.
Чтобы еще глубже разобраться в смысле остаточного члена, снова взглянем на двойную спираль в правой части рисунка 21.4. Она представляет нам функцию Li( x критическая прямая) при x = 20. Критическая прямая — испещренная, если ГР верна, всеми нетривиальными нулями дзета-функции — отображается под действием функции Li(20 z ) в спираль. Что будет, если вместо 20 мы возьмем какое-нибудь большее значение х ? Какой вид примут соответствующие спирали?
Общее представление о том, что при этом происходит, дается на рисунке 21.7. Там представлены три функции: Li(10 крит. прямая), Li(100 крит. прямая) и Li(1000 крит. прямая). Во всех трех случаях показано, как отображается один и тот же отрезок критической прямой — отрезок от 1/ 2− 5 i до 1/ 2+ 5 i .
Рисунок 21.7.Li( x критическая прямая) при x = 10, 100 и 1000. Отображаемая часть критической прямой представляет собой отрезок от 1/ 2− 5 i до 1/ 2+ 5 i .
Как видно, при увеличении x от 10 до 100 и далее до 1000 происходят следующие явления.
• Спирали растут в размере, но при этом по-прежнему сходятся к тем же двум точкам −πi и πi .
• Отрезок критической прямой, который мы отображаем (длина его равна 10 единицам), все сильнее и сильнее растягивается, накручиваясь все большее и большее число раз вокруг точек −πi и πi .
• Верхняя и нижняя спирали приближаются друг к другу, «целуются» при каком-то значении x между 100 и 1000, а после этого пересекаются (спирали в действительности «целуются», когда x = 399,6202933538…).
Выбранный нами отрезок критической прямой слишком короткий для того, чтобы достичь первой пары нулей при 1/ 2± 14,134725 i . Поскольку сама прямая растягивается, а спирали при этом, наматываясь все более и более вокруг точек −πi и πi , растут в размере, возникает интересный вопрос. Не случится ли так, что растяжение прямой и намотка спиралей удержат нули дзета-функции на небольшом удалении от точек −πi и πi независимо от того, сколь сильно увеличились спирали? Ответ — нет; по мере роста x нули дзета-функции отображаются в точки, расположенные сколь угодно далеко. Когда ρ равняется первому нулю дзета-функции (это нуль при 1/ 2+ 14,134725 i ), а аргумент x достигает скромного триллиона, функция Li (x ρ) добирается до вещественных частей, превышающих 2200.
В главе 14.vii упоминался недавний результат, полученный Бейсом и Хадсоном, — первое литлвудово нарушение (когда π(x) впервые оказывается больше чем Li (x) ) происходит до, а весьма вероятно, что и при x = 1,39822×10 316. Представим себе, что нам надо повторить весь процесс, с помощью которого мы вычислили π (1000 000), но для указанного числа (назовем его числом Бейса-Хадсона) вместо 1000 000. Какая арифметика была бы тут задействована?
Читать дальшеИнтервал:
Закладка:










