Иэн Стюарт - Истина и красота. Всемирная история симметрии.

В качестве примера представим себе астронома, который пытается вычислить движение Луны. Он запишет математические уравнения, определяющие движение Луны, и тут же застрянет, поскольку не видно никакого способа решить эти уравнения точно. Тогда наш астроном может слегка схитрить, вводя в свои уравнения различные упрощающие приближения. Математика будет волновать вопрос, могут ли эти приближения серьезно повлиять на ответ, и он будет стремиться доказать, что с ними все в порядке. У астронома же есть иной способ проверить осмысленность своих действий. Он может посмотреть, действительно ли движение Луны таково, как следует из его вычислений. Если да, то этим одновременно обосновывается метод (поскольку получается правильный ответ) и проверяется теория (по той же причине). Замкнутого логического круга здесь нет, потому что если метод математически некорректен, то почти наверняка он не позволит правильно предсказать движение Луны [6] Действительно, Луна близка и хорошо видна. Ситуация приобретает несколько большую остроту в том, например, случае, когда астроном сумел сделать лишь небольшое число наблюдений над каким-либо телом и исходя из них хочет узнать характер его дальнейшего движения. (Примеч. перев.) .

Без доступа к роскоши наблюдений или экспериментов математикам приходится проверять свою работу, исходя из ее внутренней логики. Чем важнее следствия из некоторого утверждения, тем важнее убедиться, что это утверждение истинно. Так что доказательство становится даже еще важнее, когда всем хочется, чтобы данное утверждение было верным, или когда из его истинности будет вытекать огромный объем следствий.

Доказательства не могут висеть в воздухе, и их нельзя до бесконечности возводить к другим, логически им предшествующим. Где-то у них должно быть начало, и начало это по определению состоит из вещей, которые не доказываются и никогда не будут доказываться. Сегодня мы называем эти недоказываемые исходные предположения аксиомами. Для математической теории аксиомы представляют собой правила игры.

Всякий, кто возражает против аксиом, может при желании их изменить; однако результатом таких действий будет совсем другая история. Математика не утверждает, что некоторое утверждение истинно: она утверждает, что если принять ряд предположений, то данное утверждение должно быть их логическим следствием. Отсюда не следует, что аксиомы не подлежат изменениям. Математики могут обсуждать вопрос о том, предпочтительна ли данная система аксиом по сравнению с другими в отношении тех или иных целей, или же вопрос о том, представляет ли данная система какой-нибудь интерес сама по себе. Но эти дискуссии не касаются внутренней логики любой из выбранных систем аксиом и получаемых из них следствий. Они касаются лишь того, какие из этих систем заслуживают внимания, вызывают интерес или представляют собой хорошее развлечение.

Следствия из аксиом Эвклида — длинная, тщательно отобранная цепочка логических построений — простираются необычайно далеко. Например, он доказывает — применяя логику, которая в его дни считалась безукоризненной, — что, коль скоро вы принимаете его аксиомы, вы неизбежно должны заключить следующее.

• Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов двух других его сторон.

• Существует бесконечно много простых чисел.

• Существуют иррациональные числа — такие, которые не выражаются в виде дроби. Примером является квадратный корень из двух.

• Имеется ровно пять правильных тел: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.

• Любой угол можно точно разделить на две равные части, используя только циркуль и линейку.

• Можно построить правильные многоугольники с 3, 4, 5, 6 , 8, 10 и 12 сторонами, используя только циркуль и линейку.

Я выразил эти «теоремы», как называются любые обладающие доказательством математические утверждения, на современном языке. Язык Эвклида отличался довольно сильно: Эвклид не работал непосредственно с числами. Все, что мы интерпретируем как свойства чисел, формулируется у него в терминах длин, площадей и объемов.

Содержание «Начал» разбивается на две основные категории. Имеются теоремы, говорящие нам, что некое утверждение истинно. И имеются конструкции, говорящие нам, как что-либо можно сделать.

Типичная и заслуженно знаменитая теорема — это Предложение 47 Книги I «Начал», широко известное как теорема Пифагора. Она гласит, что самая длинная сторона в прямоугольном треугольнике находится в определенной связи с двумя другими. Но без дополнительных усилий или интерпретации она не дает метода для достижения какой-либо цели.

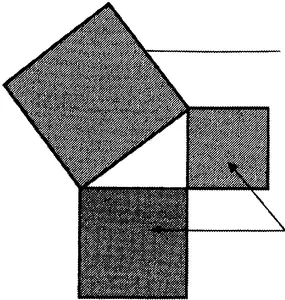
Теорема Пифагора.

Конструкция, существенная для нашего рассказа, содержится в Предложении 9 из Книги I, где Эвклид решает задачу «бисекции» (деления пополам) углов. Эвклидов метод деления угла пополам прост, но остроумен, с учетом ограниченных возможностей, доступных на той ранней стадии развития. Если задан угол (1), образованный двумя отрезками прямых, поместите циркуль в точку пересечения этих отрезков (2) и проведите окружность, которая пересечет отрезки в двух точках, по одной на каждом (черные точки). Теперь проведите (3) две окружности того же радиуса с центрами в полученных точках. Они пересекутся в двух точках (отмечена только одна из них), после чего через них проводится (4) искомая биссектриса (показана точками).

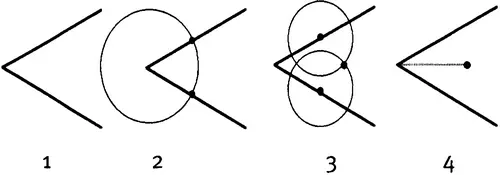
Как разделить угол пополам циркулем и линейкой.

Повторяя это построение, можно разделить угол на четыре равные части, на восемь, на шестнадцать — число частей удваивается на каждом шаге, так что мы получаем степени двойки: 2, 4, 8, 16, 32, 64 и так далее.

Как я уже говорил, в «Началах» основной аспект, имеющий отношение к нашему рассказу, состоит не в том, что там содержится, а в том, чего там нет. Эвклид не дал никаких методов для решения следующих задач.

• Деление угла точно на три равные части (трисекция угла).

• Построение правильного многоугольника с 7 сторонами.

• Построение отрезка, длина которого равна длине окружности заданного радиуса (выпрямление окружности).

• Построение квадрата, площадь которого равна площади круга заданного радиуса (квадратура круга).

• Построение куба, объем которого ровно вдвое больше объема заданного куба (удвоение куба).

Иногда говорится, что сами греки воспринимали эти упущения как недостатки в монументальном труде Эвклида и посвятили много сил их исправлению. Историки математики нашли очень мало свидетельств в поддержку этих утверждений. В действительности греки были в состоянии решить все перечисленные выше задачи, но для этого им приходилось использовать методы, находившиеся за пределами установленных Эвклидом рамок. Все эвклидовы построения выполнялись циркулем и линейкой без делений. Греческие геометры могли бы выполнить трисекцию угла, используя специальные кривые, называемые коническими сечениями; они могли бы квадрировать круг, используя другую специальную кривую, называемую квадратрисой. С другой стороны, они, кажется, не понимали, что если можно выполнить трисекцию угла, то можно построить и правильный семиугольник (да, я имею в виду именно семиугольник; девятиугольник построить несложно, а вот для семиугольника потребуется очень хитрое построение). На самом деле они, похоже, вообще не изучали следствий, вытекающих из трисекции угла. Душа их, по-видимому, не лежала к таким исследованиям.