Алексей Лосев - Хаос и структура

у = х 2 + 1

и пусть начальное значение x: будет 3. Тогда начальное значение у=3 2+1 = 10. Возьмем теперь какое–нибудь новое значение x, напр. 4, тогда y =4 2+1 = 17. В первом случае приращение будет

Δ.γ = 4 — 3 = 1,

во втором случае приращение будет

∆у— 17— 10 = 7.

Следовательно, = =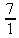7.

Будем теперь постепенно уменьшать Δx, придавая ему значения 0,9; 0,8; 0,7 и т. д. Соответственно будет меняться χ и также у, а стало быть, и 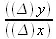. Мы действительно видим, что 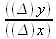принимает все меньшие и меньшие значения: 7; 6,9; 6,8; 6,7 и т. д. Спрашивается: до каких же пор будет это отношение уменьшаться? ∆х стремится к нулю. К чему же стремится ?

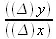Чтобы ответить на этот вопрос, представим вышеприведенное выражение — при помощи данной формулы у=χ 2+1. Именно, взявши приращенную функцию, получаем:

у+∆у=(х+∆х) 2+1 = χ 2+ 2χΔχ+(Δχ) 2+1,

откуда

∆у = х 2+ 2х∆х + (∆х) 2+1—(х 2+1) =

=χ 2+2χΔχ+(Δχ) 2+1 — χ 2 —1 = 2х ∆х+(∆х) 2.

Следовательно,

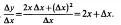
Итак, чтобы судить о том, к чему стремится 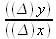, достаточно полученное выражение 2х+∆х взять в пределе, т. е. в условии стремления ∆х к нулю. Очевидно, если Ах стремится к нулю, то 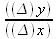стремится к 2х, так как ∆х, как стремящееся к нулю, стремится просто отпасть. Значит, если начальное значение аргумента χ у нас было 3, то предел отношения 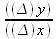будет равен, очевидно, 2–3 = 6.

И действительно, просматривая в нашей табличке значения 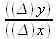, мы видим, что оно постепенно уменьшается, но не становится меньше 6. Если бы мы взяли, напр., ∆х = 0,001, то, как показывает вычисление, 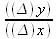оказалось бы равным 6,001. Легко проверить это, подставляя все меньшие и меньшие ∆х и получая отсюда все меньшие и меньшие 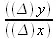, но не становящиеся меньше 6. 6—это предел, Δχ к которому стремится 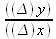если брать функцию у=х 2+1 при начальном значении х=3.

На этом простейшем примере отчетливо видно, какую форму приобретает взаимоотношение χ и у, когда оно начинает действовать не само по себе, но в своем инобытии, в своем становлении, когда они сплошно и неизменно растут или вообще меняются.

Предел этого отношения 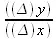, когда ∆х стремится к нулю, и есть производная, т. е. функция, «произведенная» от у, которую называют первообразной функцией. Следовательно, производная данной функции есть предел отношения приращения этой функции к приращению аргумента, когда это приращение аргумента стремится к нулю как к своему пределу.

Не будем забиваться в абстрактные дебри, как это любят делать математики, давая это понятие в дифференциальном и интегральном исчислении. Также недостаточны для понимания производной и те геометрические и механические привнесения и толкования, которыми математики уснащают свои руководства, думая на них конкретизировать это отвлеченное понятие. Надо, однако, еще до этих применений и толкований научиться понимать эту замечательную категорию, понимать всю ее жизненную и, следовательно, философскую конкретность.

Что такое производная? Для понимания этой основной категории математического анализа надо с максимальной отчетливостью представить себе разницу между бытием и инобытием или, точнее, между бытием и становлением. Если эта разница усвоена нами с достаточной отчетливостью, тогда необходимо достигнуть четкости еще в представлении того, как совершается стремление к пределу. Если эти две вещи усвоены, то логический состав производной будет ясен сам собой.

Что такое становление? Его удобно можно обрисовать путем противопоставления голому бытию (или голой идее [228] В рукописи: идеи. ), по сравнению с чем оно действительно есть резкая противоположность. Бытие есть прежде всего нечто оформленное и устойчивое; становление бесформенно стремится вперед. Бытие — царство раздельности, координированности; становление же есть алогический процесс, в котором все отдельные моменты сливаются в одну неразличимую непрерывность. Арифметика оперирует с числами вне всякой их процессуальности. Для нее они — вечные, незыблемые идеи, предстоящие в виде некоей картины, и считающий только выбирает из этой картины то одни числа, то другие. Алгебра и элементарная геометрия, не оперируя с арифметическими числами, все же, вполне на манер арифметики, оперируют со своими величинами опять–таки чисто статически. И только в анализе дана чистая стихия становления, чистое алогическое становление, в котором тонет всякая раздельность, затухает всякое оформление и совершается уход в бесконечную даль, к неохватным горизонтам.

Идеи, числа, вещи, взятые как неподвижные, статические, вечные структуры, предстоят как определенным образом связанные между собой, предстоят в некоем конкретном взаимоотношении. Будучи же погружены в стихию становления, они в корне меняют свое взаимоотношение; оно становится неузнаваемым, хотя мы и должны уметь выводить это их алогически–становя–щееся взаимоотношение из их логически–неподвижного взаимоотношения. Вещи, идеи, числа—все, что мыслится и существует, — одним образом взаимосоотносится, когда берется в чистом и непосредственном виде, и совершенно другим способом взаимосоотносится, когда уходит в алогическое становление и растворяется в нем. Итак, это первое и самое главное в производной: производная есть взаимоотношение величин, перешедших в алогическое становление.

Второе, очень важное обстоятельство заключается в том, что производная содержит в своем логическом составе момент предела. Что такое предел, об этом уже говорилось выше. Однако ни на минуту нельзя упускать из виду всего своеобразия этой богатой категории — предела и надо уметь учитывать его в общем логическом составе производной. Схематически эту ситуацию можно представить так.

Аргумент х, погрузившись в становление, меняется, движется — в бесконечность.

Зависящая от него функция у, погрузившись в становление, тоже все время меняется, движется—до бесконечности.