Яков Перельман - Математика для любознательных

Точно так же выполняются и другие действия. Для упражнения приводим далее ряд примеров, число которых читатель, при желании, может увеличить самостоятельно:

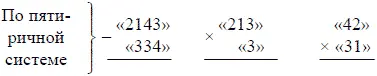
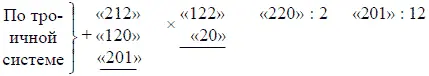
Ответы:

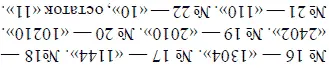
При выполнении этих действий мы сначала мысленно изображаем написанные числа в привычной нам десятичной системе, а получив результат, снова изображаем его в требуемой недесятичной системе. Но можно поступать и иначе: составить «таблицу сложения» и «таблицу умножения» в тех же системах, в которых даны нам числа, и пользоваться ими непосредственно. Например, таблица сложения в пятиричной системе такова:

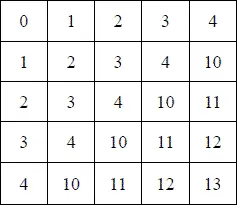
С помощью этой таблички мы могли бы сложить числа «4203» и «2132», написанные в пятиричной системе, гораздо менее напрягая внимание, чем при способе, примененном раньше.

Упрощается, как легко понять, также выполнение вычитания.

Составим и таблицу умножения («Пифагорову») для пятиричной системы.

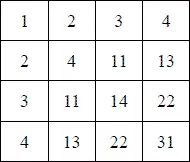
Имея эту табличку перед глазами, вы опять-таки можете облегчить себе труд умножения (и деления) чисел в пятиричной системе, - как легко убедиться, применив ее к приведенным выше примерам. Например, при умножении

рассуждаем так: трижды три «14» (из таблицы); 4 пишем, 1 - в уме. Один на 3 дает 3, да еще один, - пишем 4. Дважды три = «11»; 1 - пишем, 1 - переносим влево. Получаем в результате «1144».

Чем меньше основание системы, тем меньше и соответствующие таблицы сложения и умножения. Например, для троичной системы обе таблицы таковы:

Таблица сложения для 3-ной системы.

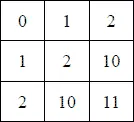
Пифагорова таблица для 3-ной системы:

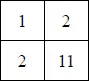
Их можно было бы сразу же запомнить и пользоваться ими для выполнения действий. Самые маленькие таблицы сложения и вычитания получаются для двоичной системы:

Таблица сложения для двоичной системы:

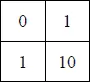
Таблица умножения для двоичной системы:

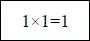
При помощи таких-то простых «таблиц» можно выполнять в двоичной системе все четыре действия! Ум - ножения в этой системе, в сущности, как бы и вовсе нет: ведь умножить на единицу значит оставить число без изменения: умножение же на «10», 100», «1000» (т. е. на 2, на 4, на 8) сводится к простому приписыванию справа соответствующего числа нулей. Что же касается сложения, то для выполнения его нужно помнить только одно - что в двоичной системе 1 + 1 = 10. Не правда ли, мы с полным основанием назвали раньше двоичную систему самой простой из всех возможных? Длинота чисел этой своеобразной арифметики искупается простотой выполнения над ними всех арифметических действий. Пусть требуется, например, умножить:

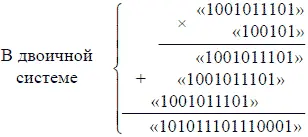
Выполнение действия сводится только к переписыванию данных чисел в надлежащем расположении: это требует несравненно меньших умственных усилий, чем умножение тех же чисел в десятичной системе (605 x 37 = 22385). Если бы у нас была принята двоичная система, изучение письменного счисления требовало бы наименьшего напряжения мысли (зато - наибольшего количества бумаги и чернил). Однако в устном счете двоичная арифметика по удобству выполнения действий значительно уступает нашей десятичной.

Не видя числа, трудно, конечно, угадать, какое оно - четное или нечетное. Но не думайте, что вы всегда сможете сказать это, едва увидите задаваемое число. Скажите, например, четное или нечетное число 16?

Если вам известно, что оно написано по десятичной системе, то, без сомнения, можно утверждать, что число это - четное. Но когда оно написано по какой-либо другой системе - можно ли быть уверенным, что оно изображает непременно четное число?

Оказывается, нет. Если основание, например, семь, то «16» означает 7 + 6 = 13, число нечетное. То же будет и для всякого нечетного основания (потому что всякое нечетное число + 6 = нечетному числу).

Отсюда вывод, что знакомый нам признак делимости на два (последняя цифра четная) безусловно пригоден только для 10-тичной системы счисления, для других же - не всегда. А именно, он верен только для систем счисления с четным основанием: 6-ричной, 8-ричной и т. п. Каков же признак делимости на 2 для систем с нечетным основанием? Достаточно краткого размышления, чтобы установить его: сумма цифр должна быть четной. Например, число «136» четное во всякой системе счисления, даже и с нечетным основанием: действительно, в последнем случае имеем: нечетные числа [63]+ нечетное число + четное = четному числу.

С такою же осторожностью надо отнестись к задаче: всегда ли число 25 делится на 5? В 7-ричной или в 8-ричной системе число, так изображенное, на 5 не делится (потому что оно равно девятнадцати или двадцати одному). Точно так же общеизвестный признак делимости на 9 (сумма цифр…) правилен только для десятичной системы. Напротив, в пятиричной системе тот же признак применим для делимости на 4, а, например, в семиричной - на 6. Так, число «323» в пятиричной системе делится на 4, потому что 3 + 2 + 3 = 8, а число «51» в семиричной - на 6 (легко убедиться, переведя числа в десятичную систему: получим соответственно 88 и 36). Почему это так, читатель сам сможет сообразить, если вникнет хорошенько в вывод признака делимости на 9 и приложит те же рассуждения, соответственно измененные, например, к семиричной системе для вывода признака делимости на 6.

Труднее доказать чисто арифметическим путем справедливость следующих положений:

Знакомые с начатками алгебры легко найдут основание, объясняющее свойство этих равенств. Остальные читатели могут проверить их рядом проб для разных систем счисления.