Яков Перельман - Математика для любознательных

Чтобы составить себе представление об огромности миллиарда, подумайте о том, что в книжке, которую вы сейчас читаете, заключается немногим более 200.000 букв. В пяти таких книжках окажется один миллион букв. А миллиард букв будет заключать в себе стопка из 5.000 экземпляров этой книжки - стопка, которая, будучи аккуратно сложена, составила бы столб высотой с Исакиевский собор.

Миллиард секунд часы отобьют более чем в 30 лет (точнее в 31,7лет). А миллиард минут составляет более 19 столетий; человечество всего двадцать четыре года назад [87](29 апреля 1902 года в 10 часов 40 мин.) начало считать второй миллиард минут от первого дня нашего летосчисления.

Ощутить огромность этих числовых исполинов трудно даже человеку, опытному в обращении с миллионами. Великан-миллион - такой же карлик рядом со сверх-великаном биллионом, как единица рядом с миллионом. Об этом взаимоотношении мы обыкновенно забываем и не делаем в своем воображении большой разницы между миллионом, биллионом и триллионом. Мы уподобляемся здесь тем первобытным народам, которые умеют считать только до 2 или до 3, а все числа свыше их одинаково обозначают словом много. «Подобно тому, как ботокудам [88]кажется несущественной разница между двумя и тремя, - говорит известный германский математик проф. Г. Шуберт, - так и многим современным культурным людям представляется несущественной разница между биллионом и триллионом. По крайней мере, они не думают о том, что одно из этих чисел в миллион раз больше другого и что, значит, первое относится ко второму приблизительно так, как расстояние от Берлина до Сан-Франциско относится к ширине улицы».

Волос, увеличенный по толщине в биллион раз, был бы раз в 8 шире земного шара, а муха при таком увеличении была бы в 70 раз толще Солнца!

Взаимоотношение между миллионом, биллионом и триллионом можно с некоторою наглядностью представить следующим образом. В Ленинграде еще недавно было миллион жителей. Вообразите же себе длинный прямой ряд городов, таких как Ленинград, - целый миллион их; в этой цепи столиц, тянущихся на семь миллионов километров (в 20 раз дальше Луны) будет насчитываться биллион жителей… Теперь вообразите, что перед вами не один такой ряд городов, а целый миллион рядов, т. е. квадрат, каждая сторона которого состоит из миллиона Ленинградов и который внутри сплошь уставлен Ленинградами: в этом квадрате будет триллион жителей.

Одним триллионом кирпичей можно было бы, размещая их плотным слоем по твердой поверхности земного шара, покрыть все материки равномерным сплошным пластом высотою с четырехэтажный дом (16 м).

Если бы все видимые в сильнейшие телескопы звезды обоих небесных полушарий, т. е. не менее 500 миллионов звезд - были обитаемы и населены каждая, как наша Земля, то на всех этих звездах, вместе взятых, насчитывался бы только один триллион людей.

Последнюю иллюстрацию мы заимствуем из мира мельчайших частиц, составляющих все тела природы - из мира молекул. Молекула по ширине меньше точки типографского шрифта этой книги примерно в миллион раз. Вообразите же триллион таких молекул [89], нанизанных вплотную на одну нитку. Какой длины была бы эта нить? Ею можно было бы семь раз обмотать земной шар по экватору!

В старинной (XVIII в.) «Арифметике» Магницкого, о которой мы не раз уже упоминали, приводится таблица названий классов чисел, доведенная до квадрильона, т. е. единицы с 24 нулями [90].

Это было большим шагом вперед по сравнению с более древним числовым инвентарем наших предков. Древняя славянская лестница больших чисел была до XV века гораздо скромнее и достигала только до ста миллионов. Вот эта старинная нумерация:

Магницкий широко раздвинул древние пределы больших чисел в своей табличке. Но он считал практически бесполезным доводить систему наименований числовых великанов чересчур далеко. Вслед за его таблицей он помещает такие стихи:

Числ есть бесконечно,

умом нам недотечно,

И никто знает конца,

кроме всех бога творца.

Несть бо нам определьно

тем же есть и безцельно

Множайших чисел искати

и больше сей писати

Превосходной таблицы

умов наших границы

И аще кому треба

счисляти что внутрь неба

Довлеет числа сего

к вещем всем мира сего.

Наш старинный математик хотел сказать этими стихами, что так как ум человеческий не может обнять бесконечного ряда чисел, то бесцельно составлять числа больше тех, которые представлены в его таблице, «умов наших границе». Заключающиеся в ней числа (от 1-цы до квадрильонов включительно) достаточны для исчисления всех вещей видимого мира, - достаточны для тех, «кому треба счисляти что внутрь неба».

Любопытно отметить, что Магницкий оказался в данном случае почти прозорливцем. По крайней мере, до самого последнего времени наука не ощущала еще нужды в числах высшего наименования, чем квадрильоны. Расстояния самых отдаленных звездных скоплений, по новейшим оценкам астрономов исчисляемые в сотни тысяч «цветовых лет» [91], в переводе на километры выражаются триллионами. Это - доступные сильнейшим телескопам видимые границы вселенной. Расстояние всех других звезд, расположенных «внутри неба», выражаются, конечно, меньшими числами. Общее чис - л о звезд исчисляется «всего лишь» сотнями миллионов. Древность старейших из них не превышает, по самой щедрой оценке, биллиона лет. Массы звезд исчисляются тысячами квадрильонов тонн.

Обращаясь в другую сторону, к миру весьма малых величин, мы и здесь не ощущаем пока надобности пользоваться числами свыше квадрильонов. Число молекул в кубическом сантиметре газа - одно из самых больших множеств, реально исчисленных, - выражается десятками триллионов. Число колебаний в секунду для самых быстроколеблющихся волн лучистой энергии (лучей Гесса) не превышает 40 триллионов. Если бы мы вздумали подсчитать, сколько капель в океане (считая даже объем капли 1 куб. миллиметр, - что весьма немного), нам и тогда не пришлось бы обратиться к наименованиям выше квадрильона, потому что число это исчисляется только тысячами квадрильонов.

И лишь при желании выразить числом, сколько граммов вещества заключает вся наша солнечная система, понадобились бы наименования выше квадрильона, потому что в числе этом 34 цифры (2 и 33 нуля): это - две тысячи квинтильонов.

Если вам интересно, каковы наименования сверх-исполинов, следующих за квадрильоном, вы найдете их в приводимой здесь табличке:

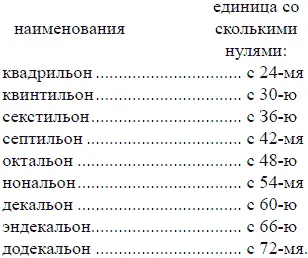
Далее наименований не имеется. Но и эти, в сущности, почти не употребляются, да и мало кому известны. Как велики выражаемые ими числа, видно хотя бы из того, что число граммов вещества во вселенной (по современным воззрениям) «всего» 10 нональонов.