Яков Перельман - Математика для любознательных

Какое число делится на все числа без остатка?

(ответ - на стр. 302).

Гулливер в своих странствованиях, покинув карликов-лилипутов, очутился среди великанов. Мы путешествуем в обратном порядке: познакомившись с числовыми исполинами, переходим к миру лилипутов, - к числам, которые во столько же раз меньше 1-цы, во сколько раз единица меньше числового великана.

Разыскать представителей этого мира не составляет никакого труда: для этого достаточно написать ряд чисел, обратных миллиону, миллиарду, биллиону и т. д., т. е. делить 1-цу на эти числа. Получающиеся дроби

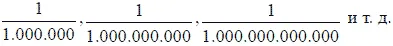
есть типичные числовые лилипуты, такие же пигмеи по сравнению с единицей, каким является единица по сравнению с миллионом, миллиардом, биллионом и прочими числовыми исполинами.

Вы видите, что каждому числу-исполину соответствует число-лилипут, и что, следовательно, числовых лилипутов существует не меньше, чем исполинов. Для них также придуман сокращенный способ обозначения. Мы уже упоминали, что весьма большие числа в научных сочинениях (по астрономии, физике) обозначаются так:

Соответственно этому, числовые лилипуты обозначаются следующим образом:

Есть ли, однако, реальная надобность в подобных дробях? Приходится ли когда-нибудь действительно иметь дело со столь мелкими долями единицы?

Об этом интересно побеседовать подробнее.

Секунда, по обычному представлению, есть настолько малый промежуток времени, что с весьма мелкими частями ее не приходится иметь дела ни при каких обстоятельствах. Легко написать - 1/ 1000секунды, - но это чисто бумажная величина, потому что ничего не может произойти в такой ничтожный промежуток времени.

Так думают многие, - но ошибаются, потому что в тысячную долю секунды могут успеть совершиться весьма различные явления. Поезд, проходящий 36 километров в час, делает в секунду 10 метров, и, следовательно, в течение 1000-й доли секунды успевает продвинуться на один сантиметр. Звук в воздухе переносится в течение 1000-й доли секунды на 33 сантиметра, а пуля, покидающая ружейный ствол со скоростью 700-800 метров в секунду, переносится за тот же промежуток времени на 70 сантиметров. Земной шар перемещается каждую 1000-ю долю секунды, в своем обращении вокруг солнца, на 30 метров. Струна, издающая высокий тон, делает в 1000-ю долю секунды 2-4 и более полных колебаний; даже комар успевает в это время взмахнуть вверх или вниз своими крылышками. Молния длится гораздо меньше 1000-й доли секунды: в течение этого промежутка времени успевает возникнуть и прекратиться столь грозное явление природы (молния простирается в длину на целые километры).

Но - возразите вы, - 1000-я доля секунды еще не подлинный лилипут, как никто не назовет тысячу числовым гигантом. Если взять миллионную долю секунды, то уж наверное можно утверждать, что это - величина нереальная, промежуток времени, в течение которого ничего произойти не может. Ошибаетесь: даже и одна миллионная доля секунды - для современного физика, например, - вовсе не чрезмерно маленький промежуток. В области явлений световых (и электрических) ученому сплошь и рядом приходится иметь дело с гораздо более мелкими частями секунды. Напомним прежде всего, что световой луч пробегает ежесекундно (в пустоте) 300.000 километров; следовательно, в 1.000.000-ю долю секунды свет успевает перенестись на расстояние 300 метров - примерно на столько же, на сколько переносится в воздухе звук в течение целой секунды.

Далее: свет есть явление волнообразное, и число световых волн, проносящихся ежесекундно через точку пространства, исчисляется сотнями биллионов. Те световые волны, которые, действуя на наш глаз, вызывают ощущение красного света, имеют частоту колебаний 400 биллионов в секунду; это значит, что в течение одной 1.000.000-й доли секунды в наш глаз вступает 400.000.000 волн, а одна волна вступает в глаз в течение 400 000 000 000 000-й доли секунды. Вот подлинный числовой лилипут!

Но этот несомненный, реально существующий лилипут является истинным великаном по сравнению с еще более мелкими долями секунды, с которыми физик встречается при изучении Рентгеновых лучей. Эти удивительные лучи, обладающие свойством проникать через многие непрозрачные тела, представляют собою, как и видимые лучи, то же волнообразное явление, но частота колебаний у них значительно больше, чем у видимых: она достигает 25000 биллионов в секунду! Волны следуют тут одна за другой в 60 раз чаще, чем в лучах видимого красного света. Лучи «гамма» и недавно открытые «космические» лучи Гесса обладают частотою еще большею, чем лучи Рентгена. Значит, и в мире лилипутов существуют свои великаны и карлики. Гулливер был выше лилипутов всего в дюжину раз и казался им великаном. Здесь же один лилипут больше другого лилипута в пять дюжин раз и, следовательно, имеет все права именоваться по отношению к нему исполином.

Интересно рассмотреть теперь, какие наименьшие расстояния приходится отмеривать и оценивать современным исследователям природы.

В метрической системе мер наименьшая единица длины для обиходного употребления - миллиметр; она примерно вдвое меньше толщины спички. Чтобы измерять предметы, видимые простым глазом, такая единица длины достаточно мелка. Но для измерения бактерий и других мелких объектов, различимых только в сильные микроскопы, миллиметр чересчур крупен. Ученые обращаются для таких измерений к более мелкой единице - микрону, который в 1000 раз меньше миллиметра. Так называемые красные кровяные тельца, которые насчитываются десятками миллионов в каждой капельке нашей крови, имеют в длину 7 микронов и в толщину 2 микрона. Стопка из 1000 таких телец имеет толщину спички.

Как ни мелок кажется нам микрон, он все же оказывается чрезмерно крупен для расстояний, которые приходится измерять современному физику. Мельчайшие, недоступные даже микроскопу частицы, молекулы, из которых состоит вещество всех тел природы, и слагающие их еще более мелкие атомы имеют размеры от одной 10000-й до одной 1000-й доли микрона. Если остановиться на последней, наибольшей величине, то и тогда окажется, что миллион таких крупинок (а мы уже знаем, как велик миллион), будучи расположен на одной прямой, вплотную друг к другу, занял бы всего лишь один миллиметр!