Майкл Шермер - Магия чисел. Ментальные вычисления в уме и другие математические фокусы

Ответ: 5395.

Метод крест-накрест немного усложняется в задачах типа «3 на 3».

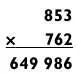
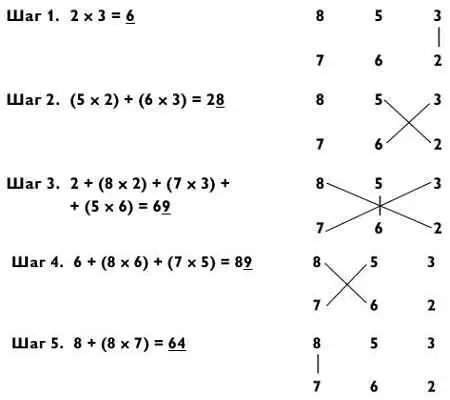
Ответ: 649 986.

Обратите внимание, что количество умножений в каждом шаге составляет 1, 2, 3, 2 и 1 соответственно. Математика, лежащая в основе метода крест-накрест, не более чем распределительный закон. Например, 853 х 762 = (800 + 50 + 3) х (700 + 60 + 2) = (3 х 2) + [(5 х 2) + (6 х 3)] х 10 + [(8 х 2) + (7 х 3) + (5 х 6)] х 100 + [(8 х 6) + (7 х 5)] х 1000 + (8 х 7) х 10 000, что в точности соответствует вычислениям по методу крест-накрест.

Можно проверить ответ с помощью модульной суммы путем перемножения модульных сумм двух чисел и вычисления модульной суммы получившегося в итоге числа. Сравните его с модульной суммой ответа. Если ответ правильный, то две модульные суммы должны совпадать. Например,

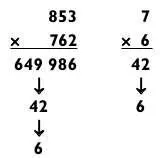
Если модульные суммы не совпадают, вы допустили ошибку. Данный метод распознает ее в среднем в 8 случаях из 9.

Что касается примера «3 на 2», процедура аналогичная, за исключением того, что вы рассматриваете сотни второго числа как нули:

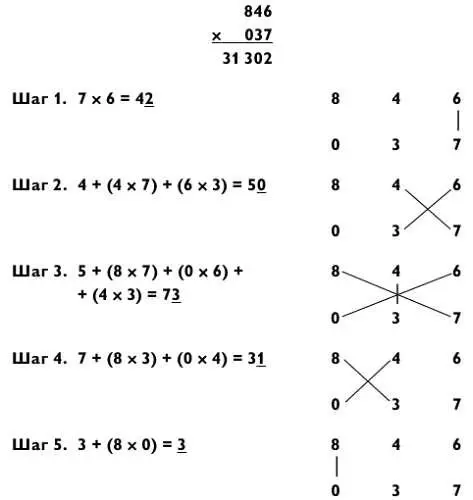
Ответ: 31 302.

Конечно, на практике, как правило, просто игнорируется умножение на нуль. Метод крест-накрест подойдет для решения задач с любым количеством цифр в числе. Например, для решения задачи «5 на 5», которая приводится ниже, потребуется девять шагов. Количество умножений на каждом шаге будет 1, 2, 3, 4, 5, 4, 3, 2, 1 (в сумме 25).

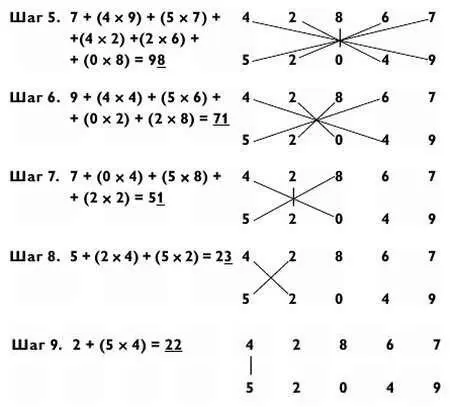
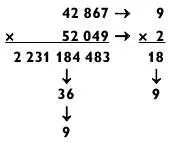
Ответ: 2 231 184 483.

Вы можете проверить ответ, используя метод модульных сумм.

* * *

Шакунтала Деви : это не поддается расчету!

В 1976 году New York Times сообщила, что индийская женщина по имени Шакунтала Деви (р. 1939) сложила 25 842 + 111 201 721 + 370 247 830 + 55 511 315, а затем умножила полученную сумму на 9878 и дала правильный ответ 5 559 369 456 432 менее чем за двадцать секунд. С трудом верится, однако, что необразованная дочь обедневших родителей сделала себе имя в Соединенных Штатах Америки и Европе в качестве молниеносного вычислителя.

К сожалению, большинство по-настоящему удивительных подвигов Деви, которые были совершены благодаря маленьким хитростям, скудно документированы. Ее величайшее заявленное достижение — умножение на время двух тринадцатизначных чисел на бумаге — появилось в Книге рекордов Гиннесса как пример «человека-компьютера». Однако время вычислений в лучшем случае вызывает сомнения. Деви, мастер метода крест-накрест, перемножила 7 686 369 774 870 х 2 465 099 745 799 — числа, как сообщается, сгенерированные случайным образом в компьютерном отделе Имперского колледжа в Лондоне 18 июня 1980 года. Правильный ответ (18 947 668 177 995 426 773 730) был, якобы, воспроизведен ею за невероятные двадцать секунд. Гиннесс предлагает следующую оговорку: «Некоторые видные математики ставят под сомнение условия, при которых это было достигнуто и предсказывают, что для нее повторить такой подвиг под чрезвычайно строгим наблюдением было бы невозможно». Поскольку Деви предстояло решить 169 задач на умножение и 167 на сложение, то есть в общей сложности выполнить 336 операций, то она должна была бы производить каждый расчет в пределах десятой доли секунды без ошибок, затрачивая время на то, чтобы записать все 26 цифр ответа. Время вычисления само по себе возводит данный рекорд в категорию «это не поддается подсчету!».

Несмотря на это, Деви подтвердила свои способности путем выполнения быстрых расчетов и даже написала об этом книгу.

Чтобы перепроверить полученный ответ другим способом, можно использовать метод, известный как сравнение по модулю 11. Он похож на метод сравнения по модулю 9 за исключением того, что здесь вы сокращаете число, поочередно вычитая и прибавляя цифры справа налево, игнорируя десятичную запятую. Если результат отрицательный, к нему надо прибавить одиннадцать. (Вам может показаться заманчивым складывать и вычитать слева направо, как в случае с модульными суммами, но чтобы метод работал, необходимо это делать справа налево.)

Например:

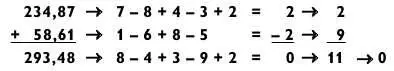
Этот же метод применим и для задач на вычитание:

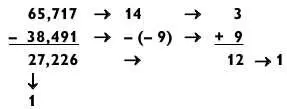
Точно так же он работает и для задач на умножение:

Если модульные числа не совпадают, значит, где-то допущена ошибка. Но даже если они совпадают, ошибка не исключена. В среднем этот метод распознает ошибку в 10 случаях из 11. Поэтому она имеет шанс пробраться сквозь караул числа одиннадцать (1 к 11) и числа девять (1 к 9), и только с шансом 1 к 99 будет незамеченной при использовании обоих типов проверки. За дополнительной информацией об этих и других очаровательных волшебных приемах предлагаю обратиться к любой из книг Мартина Гарднера по «занимательной математике» [8] См., например: Гарднер М. Математические головоломки и развлечения . М.: АСТ, Зебра, 2010. Прим. ред . .

Итак, теперь вы готовы к последней задаче на умножение в этой книге, решаемой с помощью ручки и бумаги: «10 на 10»!

Хотя в ней отсутствует какая-либо практическая ценность, кроме возможности покрасоваться! (Лично мне кажется, что умножение пятизначных чисел уже и так достаточно впечатляющее действо, особенно с тех пор, как их решение перешло в сферу ответственности калькуляторов.) Я представлю здесь этот пример только для того, чтобы доказать: это выполнимо.

Перекрестные умножения следуют тем же базовым схемам, что и при решении задачи «5 на 5». Вам предстоит девятнадцать шагов с вычислениями, а на десятом шаге — целых 10 перекрестных умножений! Поехали!

Вот как это считают:

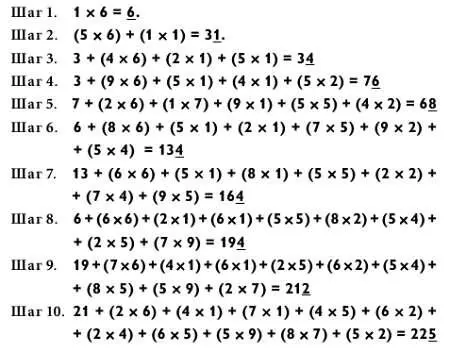
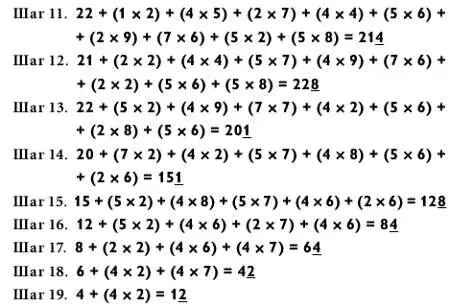
Если вы сумели договориться с этой невероятно трудной задачей с первого раза, то вы на этапе перехода из разряда подмастерья в категорию мастера математической магии!